This article by Stefan Vorkoetter originally appeared in the October 2002 issue of QuietFlyer magazine and is reproduced here with permission.

Scale Electric Airplane Design

In my March 2001 column, I wrote about selecting an electric power system for a given airplane. This month, we're going to look at designing an airplane for a given class of power system. More specifically, we'll look at choosing the scale for a scale model based on the type of power system we want to fly it with.

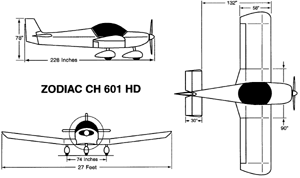
The Zenith Zodiac CH-601HD 27 foot span, two-seater home-built plane would make a great scale model subject.

The full-scale plane that we'll use as the subject of this article is the Zenith Zodiac CH-601HD, a 27-foot span, two-seat, all metal, low-wing homebuilt aircraft. Below are the basic specifications of the Zodiac, expressed both in full-scale aviation units, and units typically used by radio-control (R/C) modelers. Don't let the high wing loading scare you; the larger an airplane, the higher its wing loading can be for the same flying characteristics.

	Full Scale Units	Typical R/C Units
Wing Span	27 ft	324 in
Length	19 ft	228 in
Wing Area	130 sq.ft	18,720 sq.in
Typical Flying Weight	1,000 lb	16,000 oz
Typical Wing Loading	7.7 lb/sq.ft	123 oz/sq.ft
Power (Rotax 912)	80 hp	60,000 W
Power Loading	12.5 lb/hp	60 W/lb
Stall Speed (at 1000lb)	35 kt	40 mph
Cruise Speed	104 kt	120 mph

Scaling

The scale of a model is typically expressed as a fraction, such as 1/4, 1/8, 1/10, etc. What this means is that any linear measurement on the model is the specified fraction of the same measurement on the original. For example, in a 1/8 scale model, the wing span is 1/8 the span of the original. A 1/8 scale Zodiac would have a span of 40.5 inches, which is 1/8 of 27 feet.

Areas do not scale the same way as linear measurements. Instead, they scale according to the square of the scale factor. So, in a 1/8 scale model, any given area is 1/64 of the corresponding area on the original. Our 1/8 scale Zodiac would have a wing area of 292.5 square inches, which is 1/64 of 130 square feet.

A good set of three-views is essential to any scale project. Click to enlarge.

Volumetric, weight, and power measurements scale even more severely, by the cube of the scale factor. For a 1/8 scale model, this is a factor of 1/512. Since weight and power depend on how we build the plane and what we power it with, this factor won't determine the model's weight and power directly. Instead, it will give a guideline as to what range the weight and power should be in. For a 1/8 scale Zodiac, we can aim for a weight of about 31 oz, with a 117 Watt power system.

Because of the way that linear, area, volumetric, weight, and power measurements scale, some other parameters end up scaling in non-intuitive ways.

Power loading, which is the ratio of power to weight, is a ratio of two measurements that scale cubically. As a result, the power loading doesn't scale at all. Both the original, and our 1/8 scale model, have a 60 W/lb power loading.

Wing loading on the other hand is a ratio of weight to area, which scales by the ratio of the scale factor cubed to the scale factor squared. You may remember from your high school math that that works out to a linear factor. In other words, wing loading scales linearly. So our 1/8 scale model can be expected to have a wing loading of about 15.4 oz/sq.ft.

	Another builder's full-scale Zodiac (this is the newer XL model).

The speed required to fly level at any given angle of attack is a function of the square root of the wing loading. Since the wing loading is proportional to the scale factor, speed will be proportional to the square root of the scale factor. For our 1/8 scale model, this is 1/2.83, so we can expect a stall speed of about 14 mph, and a typical cruising speed of about 42 mph.

It's worth noting that this square root scaling of speed is what makes model airplanes appear to fly so fast, and why smaller models appear to fly even faster. Your perception of speed is based on how far the model moves compared to its own length in a given time. A large model (or full scale plane) takes more time to cover its own length than a smaller model. If you've ever watched a 747 fly overhead on final approach, you'll know that it appears to be flying impossibly slowly.

Power Based Design

Let's look at a number of possible power systems for an electric model, and from these determine the scale factors to use to build a Zenith Zodiac that will fly well on each power system. The following table gives the characteristics of seven typical brushed motor power systems:

	Motor	Battery	Propeller	Output
1	Graupner Speed 400 6V	7x500AR	6x3	48W
2	Graupner Speed 480 7.2V	7xCP1300SCR	7x4	105W
3	AstroFlight Cobalt 05	7xCP1700SCR	7x4	135W
4	Kyosho Atomic Force w/3.5:1	8xRC2000	10x7	170W
5	AstroFlight Cobalt 15G	12xRC2000	11x8	230W
6	AstroFlight Cobalt 25G	14xRC2000	11x8	290W
7	AstroFlight Cobalt 40G	20xRC2000	12x8	425W

The key to choosing a scale based on the power system is the output power relative to that of the full-size plane. Recall that power scales according to the cube of the scale factor. Therefore, the scale factor is proportional to the cube-root of the power ratio.

The next table gives the scale factor for each of the power systems above, along with some of the key specifications of the resulting model:

	1	2	3	4	5	6	7
Scale	1/10.8	1/8.3	1/7.6	1/7	1/6.4	1/5.9	1/5.2
Wing Span (in)	30	39	43	46	51	55	62
Wing Area (sq.in)	160	272	324	382	457	538	692
Weight (oz)	13	28	36	45	61	77	113
Wing Loading (oz/sq.ft)	12	15	16	17	19	21	24
Stall Speed (mph)	12	14	15	15	16	16	18
Cruise Speed (mph)	37	42	44	45	47	49	53

In theory, each of the models above, ranging from the 30 inch Speed 400 version, to the 62 inch Astro 40G model, will have roughly similar flying characteristics. In practice, the smaller models will be more responsive, and appear to fly faster, due to the square root scaling of speed discussed earlier. But the overall nature of the models should be the same.

When Things Don't Scale

There is one catch when scaling down a model, and that is a mysterious little number known as the Reynolds Number. This number depends on speed and wing chord (the distance from the leading edge to the trailing edge), and is lower for smaller models. The catch is that some airfoils' behavior changes drastically below certain Reynolds Numbers.

In other words, scaling down from full size to a model will only work up to a point. Below a certain size, the model will no longer behave like its full-scale counterpart. This is already apparent in many small models. For example, our 13 oz Speed 400 Zodiac, if we could build it that light, will readily loop from full-throttle level flight, which the full scale Zodiac won't do (nor is it certified to do so).

Scaling Weight

A real Zodiac is built primarily from aluminum sheeting, and is powered by an engine made of cast aluminum and various other metal parts. To achieve the expected scaled-down weight, we would have to build our model out of proportionally thinner aluminum, and use a scaled down version of the engine. Unfortunately, the aluminum would be too thin to hold its shape, and using a scaled down engine is not allowed because we are electric modelers.

The good news is that we can build our model out of balsa wood, foam, or fiberglass, and power it with an electric motor and a lump of nickel-cadmium (NiCd) or nickel-metal-hydride (NiMH) cells, and still end up with a model that comes out to approximately the expected scale weight.

Tuning the Power System

Having chosen a power system, and then a scale factor based on the cube root of the power ratio, we'll probably have to fine tune the power system a bit. Just because we have the right number of Watts per pound doesn't mean the plane will fly well. We need to choose the right propeller to get the right trade-off between thrust and pitch speed.

This 3/4 scale Ace PuddleMaster copy flies well using a 6V Speed 400 motor, 7x1100AAU NiCd battery, and 5.5x4 propeller.

If the propeller is large but low-pitched, we'll have plenty of thrust, but we'll run out of steam before we reach flying speed. A small but high-pitched propeller will provide plenty of power at high speed, but there won't be enough thrust to accelerate to flying speed in the first place.

The right propeller is one whose static (i.e. measured with the plane stationary) pitch speed is approximately equal to the 2.5 to 3 times the stall speed. (Pitch speed in mph is the propeller pitch in inches, multiplied by rpm, times 0.000947.) The trick is to find a propeller with the right pitch and diameter combination to achieve this at the specified power level.

Speaking of power levels, remember that the power used in the scaling calculations is the motor's output power. We have to divide that by the motor's efficiency (expressed as a decimal fraction) to find the desired input power. For example, the 135W Astro 05 system will require about 169W input, assuming a motor efficiency of 80% (or 0.8). On seven cells at about 1.1V per cell under load, that results in a current draw of about 22A (because 22A times 7.7V equals 169W).

Still using the Astro 05 system as an example, for a 1/7.6 scale Zodiac, a 7.5x3.5 propeller happens to be about right, producing a pitch speed of 45 mph at about 24A. Experimenting with different propellers in that size range should produce one that gives the desired performance. Programs like MotoCalc or ElectriCalc can help in narrowing down the choices (that's how I arrived at the 7.5x3.5 propeller choice).

	This is my Speed 600 powered Vernon Williams' Fred's Special, back when I first completed it in 1997.

Scaling Models

The technique we've just looked at isn't limited to designing a scale model from a full-sized prototype. It can also be applied to building a larger or smaller version of an existing model. Simply treat the existing model as if it were full-size, and follow all the same steps.

For example, the Ace PuddleMaster is designed to be powered by an 05 sized "can" motor turning a 7x4 prop from a 7-cell pack (RC2400 these days, but 1200SCR when the model was first made available). Such a power system produces about 100W of motor output power.

A Speed 400 power system using 1100AAU cells (instead of 500AR) produces about 42W of output power, for a power ratio of 0.42. The cube root of 0.42 is roughly 0.75, or 3/4. This means that a 3/4 "scale" model of a PuddleMaster would fly on the Speed 400 system about as well as the original would on the 05 "can" system. The following table gives the specifications for the original and a 3/4 scale model:

	Original	3/4 Scale
Scale	1/1	3/4
Wing Span (in)	48	36
Wing Area (sq.in)	402	226
Weight (oz)	44	19
Wing Loading (oz/sq.ft)	17	12

I built such a mini-PuddleMaster, powered by a Speed 400 6V motor, 7x1100AAU battery, and a 5.5x4 propeller. The wing was a tiny bit smaller (216 sq.in), and the weight a bit higher (21 oz), but it flies well.

	My Sydney's Special is a Speed 400 powered 3/4 scale copy of the Fred's Special. It has the same forgiving flying characteristics of its larger sibling.

I've also built a scaled down version of my all-time favorite plane, Vernon Williams' Fred's Special. It too is designed for 05 power, and I built a 3/4 scale version for Speed 400 power. Unlike the PuddleMaster though, my Speed 400 model came out lighter than planned, so performance was slightly better than the original.

Brushless

All of the power systems I used in the scaling examples were brushed, simply to get roughly comparable motor efficiencies. A brushless power system works just as well in this technique, the only difference being a higher efficiency. This just means that for a given output power level, less input power is needed, which equates to lighter cells and/or longer run-time.

Other Articles of Interest

• Choosing a Power System
• Electric Flight Rules of Thumb

 

Buy Stefan a coffee! If you've found this article useful, consider leaving a donation to help support stefanv.com

 

Last updated Monday July 19, 2010.

E-mail Stefan

 

Disclaimer: Although every effort has been made to ensure accuracy and reliability, the information on this web page is presented without warranty of any kind, and Stefan Vorkoetter assumes no liability for direct or consequential damages caused by its use. It is up to you, the reader, to determine the suitability of, and assume responsibility for, the use of this information. Copyright: All materials on this web site, including the text, images, and HTML mark-up, are Copyright © 2010 by Stefan Vorkoetter unless otherwise noted. All rights reserved. Unauthorized duplication prohibited. You may link to this site or pages within it, but you may not link directly to images on this site, and you may not copy any material from this site to another web site or other publication without express written permission. You may make copies for your own personal use. The text and images of this article are Copyright © 2002 by Kiona Publishing, and are reproduced here with permission. All rights reserved.