Motor Math
April 1, 2002 for Sailplane & Electric Modeler Magazine
Don’t let the word "math" in the title scare you. There won’t be much of it, but I thought it would be worthwhile explaining just how one can calculate the performance of a motor.
Last month, we looked at propeller basics (I cleverly left the word "math" out of the title that time), and one of the things we came up with was the following formula:
power = k rpm3 diameter4 pitch
This formula expresses the relationship between a propeller’s pitch, diameter, rpm, and other characteristics (represented by fudge factor k). For an average propeller, k is about 5.3×10-15 if pitch and diameter are in inches, and power is in Watts.
The power term in the formula is the amount of power needed to turn the propeller at the specified rpm. In other words, it is the required propeller input power. Since the propeller is attached to the motor shaft (we’ll only consider direct-drive for now), the propeller’s input power must equal the motor’s output power.
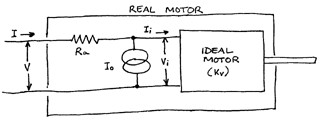
The Ideal Motor
If there were such a thing as a perfect 100% efficient motor, then the motor’s output power would be equal to the motor’s input power. In other words, all the Watts flowing into the motor would make it to the propeller, and hence become the propeller’s input power.
In reality, there are many losses built into a motor. Some of these are electrical losses, such as the resistance of the windings and brushes. Some are magnetic losses, such as the armature’s resistance to being magnetized by current flowing through the windings. There are also mechanical losses, such as brush and bearing friction, and drag as the armature rotates through the air inside the motor.
The Real Motor
For the purpose of predicting motor performance, a real motor can be treated as if it consisted of three components: an ideal motor, a resistor, and a current sink. The sketch below illustrates this. Note that this is not really what’s inside a motor, but rather is just a circuit that approximates the characteristics of a motor.
The ideal motor has only one characteristic, and that is the rpm it produces per Volt of input. This is universally known by the symbol Kv, and is expressed in rpm/Volt. (Actually, there is a second characteristic, Kt, which is the amount of torque the motor produces per Amp of input, but this is always inversely related to Kv, so if you know Kv, you can compute Kt and vice versa. The equation relating these two is Kv Kt = 1355 when Kt is expressed in inch-ounces per Amp).
The resistor also has one characteristic, its resistance, measured in Ohms. The resistor represents the winding resistance of the real motor, which is known by the symbol Ra (the "a" stands for armature). The resistance serves no useful purpose, but is an unavoidable physical attribute of the motor.
Finally, the current sink draws a fixed amount of current, and throws it away. The amount of current it draws is the no-load current of the real motor, which is known by the symbol I0 (I is the universal symbol for current, and the “0” refers to zero load). This is measured in Amps.
Now lets see how these all fit together.
First we need to know the voltage reaching the ideal motor, which we’ll call Vi ("i" for ideal). This equals the voltage at the real motor terminals (we’ll call it V), minus the voltage lost in the resistor. This in turn is equal to the total current (which we’ll call I) times the value of the resistor. So,
Vi = V – I Ra.
Next we’ll need the current reaching the ideal motor, Ii. The total current flowing into the real motor is divided between the current sink and the ideal motor. Since the current sink draws a fixed amount of current, the current reaching the ideal motor is just,
Ii = I – I0.
Now that we have the voltage and current flowing into the ideal motor, we can multiply them together to get the power. Furthermore, since the ideal motor is 100% efficient, the power flowing into it equals the power used by the propeller. So,
(V – I Ra) (I – I0) = k rpm3 diameter4 pitch.
Finally, we need to make use of the motor’s Kv value somewhere in our formulae. The ideal motor spins at an rpm directly proportional to the voltage it receives (Vi). Therefore,
rpm = (V – I Ra) Kv.
These last two equations form the basis of any calculations we may wish to perform for a motor. We have nine variables and two equations, so if we know the values for any seven of these variables, we can solve for the other two. Fortunately, we generally know everything except rpm and I.
An Example
Let’s consider a common example, an Astroflight Cobalt 05 motor, 8×4 propeller, and seven SCR type cells. For this motor, we can look up the following: Kv=2125, I0=2.5, and Ra=0.045. We’ll assume that under load, seven SCR cells will deliver about 7V. For k, we’ll use the value for an average propeller, which is 5.3×10-15. Our diameter and pitch are 8 and 4 respectively. What we want to find out is the current and the rpm. So if we plug all the numbers we know into our two equations, we get:
(7 – 0.045 I) (I – 2.5) = 5.3×10-15 rpm3 x 84 x 4
rpm = (7 – 0.045 I) x 2125
Unfortunately, solving these is non-trivial. The easiest way is with a mathematical software package such as Maple, but most of us don’t have such a program. If you’re mathematically inclined and very patient, you can solve them by hand, either symbolically or numerically.
Trial and error is a viable method too. Simply guess a value for I, and use the second equation to compute rpm. Then substitute your guessed I and computed rpm into the first equation and see if it holds true. For example, if we guess that I is 22 Amps, then the second equation gives us that rpm is 12771. If we put these values into the first equation, we get 117.2 = 180.9, which is clearly not true. So, we’ll need to try a different guess for I. If that makes the first equation worse, then we’ll need to go the other way in guessing I. After repeating this a few times, we’ll find that I is 29.4, and rpm is 12067.
Complications
These equations are adequate for getting an approximate prediction of motor performance with a given propeller, but there are a few shortcomings. In the real world, the voltage V is not known exactly, because it actually depends on the current I. The higher the current, the lower the voltage, due to the internal resistance of the cells, and also the speed control. The principals are still the same, but solving the equations becomes much more complicated.
Specialized electric flight software packages, such as MotoCalc or ElectriCalc take all these factors into account and eliminate the need for the electric modeler to solve these equations directly.
Conclusion
You certainly don’t need to know all this to successfully fly electric models, but if you like to experiment with power systems, or are designing your own models, a basic understanding of the underlying mathematics can make life a lot easier.
Related Articles
If you've found this article useful, you may also be interested in:

If you've found this article useful, consider leaving a donation in Stefan's memory to help support stefanv.com
Disclaimer: Although every effort has been made to ensure accuracy and reliability, the information on this web page is presented without warranty of any kind, and Stefan Vorkoetter assumes no liability for direct or consequential damages caused by its use. It is up to you, the reader, to determine the suitability of, and assume responsibility for, the use of this information. Links to Amazon.com merchandise are provided in association with Amazon.com. Links to eBay searches are provided in association with the eBay partner network.
Copyright: All materials on this web site, including the text, images, and mark-up, are Copyright © 2025 by Stefan Vorkoetter unless otherwise noted. All rights reserved. Unauthorized duplication prohibited. You may link to this site or pages within it, but you may not link directly to images on this site, and you may not copy any material from this site to another web site or other publication without express written permission. You may make copies for your own personal use.
Isak
August 26, 2008
Superb article!
nik
November 03, 2008
Unless I’m missing something, solving for I and rpm in those equations is actually, more or less trivial.
Stefan Vorkoetter
November 03, 2008
Nik, I assume you’re referring to the last two equations in "The Real Motor" section. The two equations have to be solved simultaneously. Solving for I or rpm in either equation alone is trivial, but solving for both I and rpm simultaneously in both equations is very difficult.
Luke F
January 01, 2010
Here’s how I think you can solve simultaneously: Stick the value of rpm (in terms of I) from equation 2 into equation 1. In other words, (7 – 0.045 I) (I – 2.5) = 5.3×10-15 [(7 – 0.045 I) x 2125]^3 x 84 x 4. Open out the brackets on the left hand side, and the cubed term in the right hand side, and move everything to the left, so you get something that looks like aI^3 + bI^2 + cI + d = 0. Then you can solve this cubic equation(*) to find a value for I, and plug into equation 2 to get a value for rpm.
To solve the cubic equation, you could either use a reasonably powerful graphical calculator (for example my casio 991ES does it), or else plot the graph in microsoft excel and see where it cuts the x-axis. It might give up to three solutions for I since it’s a cubic equation, so in that case choose the I that is most reasonable (for example you might get positive and negative values, in which case choose the positive one). There’s also an equation to find the roots of a cubic equation (similar to the one you use for quadratic equations, -b+/- root(b^2-4ac)/2a, you know the one), but it’s pretty complicated for cubic equations. But anyway, that’s how you can take the guesswork out of it!
Stefan Vorkoetter
January 01, 2010
Hi Luke. Don’t get me wrong; I didn’t say these are impossible to solve, just non-trivial for the average non-mathematical hobbyist who hasn’t done any of this stuff since high school. Your approach is definitely the way to go if you’re comfortable with it, and is what I would do.
Luke F
January 02, 2010
You’re right about that! Generally when we get to problems of this magnitude we stick them in excel and use goalseek or solver -that way we let the computer do all the number crunching and still get a reasonably accurate solution without any effort. But like you said, beyond what most hobbyists will be willing to do. Plus I agree that it’s not worth the effort considering that you could simply use a DC clamp-meter (so that you eliminate the series resistance of an ordinary Ammeter) and tachometer and get readings from those…
Bagrat Papikyan
February 10, 2011
I am in the process of making a model plane and it really helped me!
Lawrie Henrickson
June 19, 2011
You are a GOD! I have been looking for this information for years! Have you considered including the static thrust predictor equation too (which I subsequently found after locating your post): T = Kt x rpm^2 x D^3 x P. With these two equations we can calculate almost anything we need for electric set-ups!
Ganesh
April 27, 2019
Lawrie, this is Ganesh and i had another post going in the previous thread using another formula – pls check http://www.stefanv.com/rcstuff/qf200203.html#comment-476581 at the end for my comment.
Wanted to know what the value for Kt here is – in your equation. If i use 0.015 it feels like a magic number coz it gives me a thrust of 104 gms which is i guess is possibly more realistic to the motor i have (racerstar 8520 with hubsan propellers). And in reality they may end up lifting only 30 to 40 gms for various other reasons but just wanted to know the background to this predictor equation you’ve posted above. Kindly advise.
Here is my calculation.
kt 0.015
rpm^2 2862250000
D^3 16.75834871
P 51.33783305
Thrust therefore is = 3.693750691 ounces = 104.7178321 gms
Thanks.
Akis Tzortzis
February 10, 2021
Hello, I am trying (unsuccessfully) to go from RPM and Watts, to Thrust. In your example above you calculated 12067 RPM and 150W and 29A, with an 8 x 4 prop. How much thrust will that generate? Many thanks
Jon A. Jacobsen
October 24, 2023
Hi Stefan. Just reading Your article about electric motors en propeller for model airplane I wonder if there is a relationship beetwen the motors used efect (W) and the thrust of the propeller given by a mathematic formula (or emperical formula).
Kind regards
Jon A. Jacobsen
Norway