This article by Stefan Vorkoetter originally appeared in the March 2002 issue of QuietFlyer magazine and is reproduced here with permission.

Propeller Basics

The majority of powered model airplanes use a propeller as part of their power system, and electric models are no exception. Some models use a ducted fan to simulate jet flight, and some even use propane or kerosene powered turbines (real jet engines). There are also a very few models that use flapping wings as a source of motive power (known as ornithopters). However, propellers are still the most efficient way to power a model.

What Does a Propeller Do?

In short, a propeller moves air. It converts the torque of its power source (a motor or engine) into thrust, and the rotational speed (rpm) into linear speed. The combination of an electric motor and a propeller turns current (Amps) into thrust and voltage into speed.

There are two values that express the most important characteristics of all propellers: diameter and pitch. The diameter is really the diameter of the circle in which the propeller rotates. This corresponds to twice the distance from the center of the propeller hub to the tip of one blade (for a propeller with an even number of blades, that's just the distance from tip to opposite tip).

	Slicing the end off of a propeller blade reveals an airfoil just like that found on a wing. Different propellers use different airfoils. Some modern electric flight propellers have undercambered airfoils. This glow propeller has a flat-bottomed airfoil.

The pitch is a measure of how far the propeller would move forwards in one revolution if it were treated as a screw and screwed into some solid material.

Although the measure of pitch treats the propeller as if it were a screw, one shouldn't think of it as an airscrew (the name of a certain model airplane prop manufacturer notwithstanding). It is really a rotating wing, and if you were to take a propeller and slice it across the blade, you'd see a typical airfoil cross-section.

The size of a propeller is usually expressed in the form diameter x pitch. For example, an 8x4 propeller has an 8 inch diameter and 4 inch pitch.

As a very rough approximation, the diameter of the propeller controls the thrust produced, and the pitch controls the speed of the air leaving the back of the propeller. In reality, pitch also affects thrust somewhat, but thinking of the two separately helps to envision how propeller changes will affect performance.

Measuring Pitch

Most propellers are labeled with their pitch and diameter, but it is possible to determine both given an umarked prop. The diameter is straightforward to measure of course.

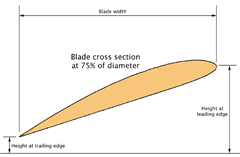
Measurements needed to determine the pitch of a propeller should be taken 3/4 of the way from the hub to the tip. Click to enlarge.

To measure the pitch, lay the propeller flat on a table, measure 75% of the way from the hub to the tip, and draw a line across the propeller blade. Measure the width of the blade at this point, along the surface of the table (i.e. the width of the blade's shadow if there were a light on the ceiling overhead). Next, measure the height of the front and the back of the blade, and compute the difference between these two to determine the height.

The pitch is then given by the formula:

pitch = 2.36 diameter height/width

There's nothing magical about the number 2.36; it's just 75% of π (pi), because we're measuring pitch at the 75% diameter mark.

The reason we measure pitch at 75% of the diameter is two-fold. Generally, the pitch of a propeller is not completely constant, varying somewhat from hub to tip to optimize it for the different linear speeds at each point along the blade. The pitch at 75% corresponds roughly to the average effective pitch of the propeller. Secondly, the propeller is sufficiently wide at 75% to allow one to get reasonably accurate measurements of blade width and height.

	Measuring the pitch of a propeller is easily done on a flat surface with an accurate ruler.

Power Requirements

Both pitch and diameter affect how much output power the motor must produce to turn the propeller at a given rpm. The following equation shows the relationship between motor output power (also called shaft power, or propeller input power), rpm, pitch, and diameter:

power = k rpm³ diameter⁴ pitch

The factor k depends on the units used to express power, pitch, and diameter, and also on characteristics of the propeller such as the airfoil it uses, its overall shape, thickness, and so on. For power in Watts, and diameter and pitch in inches, k is about 5.3x10^-15 for an average model airplane propeller.

This formula tells us a number of things. First, it tells us that rpm is not directly proportional to power. Doubling the shaft power and keeping pitch and diameter the same will only increase rpm by a factor of 1.26 (the cube root of 2).

It also tells us that increasing the pitch slightly will increase the power requirements slightly, whereas a slight increase in diameter will result in a dramatic increase in power needed to maintain the same rpm. For example, going from a 10 inch propeller to an 11 inch propeller of the same diameter would require 1.46 times the power to maintain the same rpm (11/10 to the fourth power). Or, if the shaft power were kept the same, the rpm would drop to 88% of what it was (the reciprocal of the cube root of 1.46 from the previous result).

The fact that pitch affects power requirements only slightly is very important, because it means that we can make small changes in pitch to improve model performance without having to worry too much about increasing current. For example, if we have a model with a 10x7 prop that has good take-off and climb performance, but poor high-speed performance, we can switch to a 10x8 prop and only increase power required by about 14%. Assuming the motor is near its maximum efficiency point, current will also increase by about 14%, say from 25A to 29A. Larger changes in pitch should be accompanied by a slight reduction in diameter to keep the current levels reasonable.

In practice, changing from one propeller to another will change both the rpm and the power. This is because changing the load on a motor shaft will change the rpm, which will change the power required, which will change the rpm, and so on. The motor and propeller combination will find a new operating point at which the shaft power produced equals the propeller input power required. Next month, I'll talk about how motor output power is related to input voltage, current, and rpm, and how this can be mathematically connected to the propeller formula above to predict what will actually happen.

Airflow

As was mentioned earlier, a propeller is really a rotating wing, and as such, is subject to the same aerodynamic effects as a wing. As a propeller rotates, the blades meet the oncoming air. The angle at which this happens is a function of how fast the air is moving towards the propeller and how fast the propeller is turning. If the air were stationary, the angle of attack of a given section of the blade would be exactly equal to the blade angle at that point.

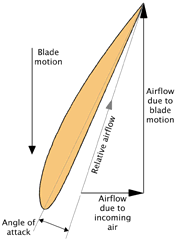
The relative angle of attack of the airflow to the propeller blade depends on the rotational speed of the blade, and the speed of the incoming air flow. Click to enlarge.

In reality, the air is not stationary, even if the plane is not moving, because the air accelerates before it reaches the propeller. As a result, from the blade's point of view, the air is meeting it at some relatively low angle, which is the blade's angle of attack.

Like any wing, a propeller blade can stall if the angle of attack is too high. This can happen with a very highly pitched blade when moving at too low an airspeed. It is for this reason that high pitch propellers, like a 10x9 or 12x12 often exhibit poor performance at low airspeeds. A plane equipped with such a propeller will often exhibit poor launch or take-off performance, and then come alive once the model is up to speed.

Also like a wing, if the angle is too low, no lift will be produced. A low pitched propeller on a fast plane (for example, 8x3, 12x5, etc.) can get to the point where it produces no thrust (in a dive, when gravity is providing the force to keep the plane moving). In high speed level flight, thrust from such a propeller can drop too low to overcome drag long before the plane has reached its designed flying speed. According to Astroflight's Bob Boucher, such propellers should be relegated to stirring paint. Of course, this statement was made in the days before slow-flyer models, which often sport very large low pitch props.

For many aircraft, a good compromise is a propeller with a diameter to pitch ratio of about 3:2 or 4:3 (for example, 8x6, 9x6, 10x7, 11x8, 12x8, 12x9, and so on). Such a propeller will become unstalled at relatively low airspeeds (usually below the model's stall speed), and will remain efficient at relatively high flying speeds.

In many full scale aircraft, the propeller has in-flight adjustable pitch, so that it can have a low pitch for maximum take-off thrust, and a higher pitch for optimal cruising efficiency. Some small full-scale aircraft can be fitted with one of three different propellers depending on the need at the time: low pitch for getting heavy loads off the ground but slow cruising, standard for general use, or high pitch for light loads but fast cruising.

Three or More Blades

Most model propellers have only two blades because a two bladed propeller is generally more efficient than a larger propeller that produces the same thrust and air speed. A common misconception is that this is due to the blades operating in each others' wakes, but this is only a small factor. Remember that the air in which the propeller is turning is moving away from the back of the propeller, so the wake from each blade will move backwards too, leaving clean air for the next blade to bite into. A reasonably pitched propeller would have to have a large number of blades before they start interfering with each others' air.

That being said however, a multi-bladed prop does have more induced drag caused by tip vortices (air spilling over the blade tips, just like wingtip vortices on a wing), because there are more tips. So, overall efficiency is lower, in much the same way that a biplane (even one without struts and bracing wires) is less efficient than a monoplane with the same wing area. A multi-bladed prop often has a larger total blade surface area than the equivalent larger two-bladed prop, further reducing efficiency (due to parasite drag).

	For best performance, reduced noise, and increased motor life, all propellers should be balanced before use. I use a Top Flite magnetic balancer, which due to its nearly frictionless bearings, will show even the slightest imbalance.

Multi-bladed propellers do have the ability to turn power into thrust and airspeed in less space than a larger two-bladed prop though, which makes them advantageous when ground clearance is an issue (or fuselage clearance for wing or pylon mounted propellers).

Practical Considerations - Balancing

As electric flyers, balancing a propeller is very important. It's important on glow powered models too, but the result of an unbalanced propeller is a lot less apparent, due to the noise and vibration of the engine. On an electric model, an unbalanced propeller is far noisier than a balanced one. Furthermore, an unbalanced propeller wastes power, because it is putting a sideways force on the motor shaft, pushing it against one side of the bearing. It also can also cause the shaft to bend somewhat, which means the motor armature (in a direct drive application) runs off-center, further reducing efficiency.

I use a Top Flite magnetic balancer, and sand material off the back side of the heavy blade as close to the tip as possible (the further from the center you remove material, the less you will have to remove). One of my direct drive models which sounds like a glow model when flown with an unbalanced prop, becomes inaudible at 200 feet when flown with a well balanced prop of the same brand.

Making It Turn

A propeller with no source of power is useless, so next month we'll look at how an electric motor interacts with the propeller to convert electric power to the form that we need it for flight, namely thrust and airspeed.

 

Buy Stefan a coffee! If you've found this article useful, consider leaving a donation to help support stefanv.com

 

Last updated Monday July 19, 2010.

E-mail Stefan

 

Disclaimer: Although every effort has been made to ensure accuracy and reliability, the information on this web page is presented without warranty of any kind, and Stefan Vorkoetter assumes no liability for direct or consequential damages caused by its use. It is up to you, the reader, to determine the suitability of, and assume responsibility for, the use of this information. Copyright: All materials on this web site, including the text, images, and HTML mark-up, are Copyright © 2010 by Stefan Vorkoetter unless otherwise noted. All rights reserved. Unauthorized duplication prohibited. You may link to this site or pages within it, but you may not link directly to images on this site, and you may not copy any material from this site to another web site or other publication without express written permission. You may make copies for your own personal use. The text and images of this article are Copyright © 2002 by Kiona Publishing, and are reproduced here with permission. All rights reserved.