Subscribe Recommend		Calculator side of the Aero Products Research E6-B9 flight computer. A Tale of Two Whiz Wheels: E6-B versus CR Wind Solutions Solving the wind triangle is the only non-trivial math needed by the private pilot. Unlike weight-and-balance or speed-time-distance calculations which are just simple arithmetic, the wind triangle requires trigonometry. At least it would require trigonometry if you didn't use some sort of flight computer, either electronic or one of the traditional "whiz-wheels". When I first began my flight training, we were all required to purchase an E6-B style flight computer. This has a circular slide rule for speed-time-distance and density altitude calculations on one side, and a graphical wind triangle solution on the other side. This style of computer is manufactured by several companies, including Aero Products Research and Jeppesen. The wind solution involves a rotating compass ring with a transparent screen and a sliding plate imprinted with diverging lines that intersect a series of concentric arcs. One literally "draws" the wind triangle on the computer and reads off the solution.    Calculator side of the Jeppesen CR-3 flight computer. After graduating with Private Pilot License in hand, I soon discovered there was a different type of non-electronic flight computer available, the Jeppesen CR-3 (and its smaller cousins, the CR-2 and CR-5). The front side of the CR-3 is similar to that of the E6-B, albeit with quite a few additional features not normally used by the private pilot, such as pressure pattern navigation and Mach number. Like the E6-B, the reverse side of the CR-3 is used to solve wind triangles, but in a very different way. Jeppesen's design, dating from 1955, provides a wind solution that doesn't require any sliding parts. It takes about the same number of steps, but they are quite different than those performed on the E6-B. The rest of this article compares the wind triangle solutions of these two flight computers. To the best of my knowledge, these are the only two non-electronic solutions used in aviation.    The components of the wind triangle. Ground speed and true heading are what we need to find. Click to enlarge. The Wind Triangle To compare the E6-B and CR computers, we first need a clear understanding of the problem they are designed to solve. When flying from one point to another, we first determine the direction of the second point relative to the first with a chart and navigation protractor. This is our desired true course. If there were no wind, we could then point the airplane in that direction and fly straight there. Unfortunately, there's usually a wind, and it's usually coming from one side or the other, meaning that it will blow us off course. To adjust for this, we point the airplane in a different direction (our heading) and let the wind blow us on course. Usually, some component of the wind also acts in a direction parallel to our line of flight, either slowing down (a headwind) or speeding up (a tailwind) our progress over the ground. This in turn affects the time it will take to get where we're going, and thus also the amount of fuel needed. Given the speed and direction of the wind (from forecasts), our desired course, and our true airspeed (from the airplane's flight manual), the wind triangle solution tells us the necessary heading to use, and what our groundspeed will be. This can be solved mathematically using the trigonometry we learned in high school. Modern electronic flight computers do exactly that behind the scenes. But the older "whiz wheel" type of flight computers can solve it almost as easily, and at the same time provide you with a picture of what's going on. A Sample Problem I'll use the following example problem to show how each type of flight computer is used to solve it: True course to our destination: 240° True airspeed from flight manual: 115kt Forecast wind at our altitude: 290° at 30kt. 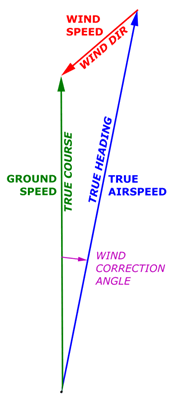The wind triangle drawing above right is actually drawn to scale for this particular sample problem.    The wind arrow is 30 kt long, pointing into the centre from a heading of 290° The E6-B Solution I'll show the E6-B solution first, because it illustrates more of the entire wind triangle than the CR solution. 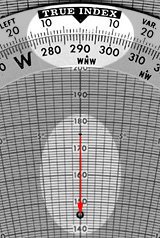The first step is to plot the wind arrow on the screen of the E6-B. First rotate the bezel so that the wind direction (290°) appears under the "True Index" mark. Then move the slide until the "grommet" in the centre is over any convenient arc (I usually use one of the 5 knot increments, e.g. 145, 155, etc.). Draw the wind arrow starting 30kt further up the slider, pointing into the grommet (click on the picture for a better view). At this point you're half way to the answer.    Rotate the bezel to 240° and move the slider until the arrow tail is on the 115kt arc. Next, rotate the bezel so the desired true course (240°) appears under the "True Index" mark. Then slide the slider until the tail of the arrow is on the arc corresponding to the true airspeed. At this point, we have our answers. The wind correction angle is given by the radial line where the tail of the arrow is. In our example, it's half way between the 11° and 12° lines, so our wind correction (crab) angle is 11.5°. The arrow tail is on our right, so our wind correction will be to the right, meaning we have to add the 11.5° to our desired 240° course, giving a 251.5° heading (this is a true heading, so don't forget to correct for magnetic variation before setting off). The arc appearing within the grommet gives our ground speed. In this example, it's 93kt, meaning we've lost 22kt due to the combined effect of the headwind component of the 30kt wind and our crab angle. Using this ground speed and the distance, we can compute the flying time and fuel needed. Although I'm mathematically inclined, the operation of the E6-B seemed a bit magical to me at first, until I realized that it literally helps you "draw" the wind triangle to scale and then take measurements from it. After looking at this illustration for a while, it becomes quite obvious.    Select the true course, draw the wind arrow, and determine crosswind and headwind (or tailwind) components. The Jeppesen CR Solution When I first saw a Jeppesen CR-3 flight computer, I was intrigued by the fact that it could do a wind solution with no slide. The solution requires about the same amount of work as using the E6-B, but the steps are different. The first step is to rotate the translucent wheel so the desired true course (240°, in green) is over the "TC" marker. Now find the green radial line corresponding to the wind direction (290°) and locate where it intersects with the green circle corresponding to the wind speed (30kt). Draw the wind arrow or just place a dot at the tail of the arrow. You can now read off the crosswind and headwind (or tailwind) components directly using the grid lines on the fixed background. In our example, the crosswind is about 23kt, and the headwind is about 19kt.    Select the true airspeed, and find the wind correction angle next to the crosswind component on the outer disk. Next, rotate the outer disk so that the true airspeed (115kt) appears over the "TAS" marker. Now find the crosswind (as determined previously) on the outer disk, and read off the wind correction angle. Here the 23 on the outer disk is half way between 11° and 12° on the inner disk, so our wind correction (crab) angle is 11.5°. Since we have a right crosswind, the correction is to the right so we add it to our 240° course, giving a 251.5° heading. Not surprisingly, this is the same answer that the E6-B gives (again, this is a true heading; you'll still need to adjust for magnetic variation). The last step is to compute ground speed. Unfortunately, it's not as simple as subtracting the headwind component from (or adding a tailwind component to) the airspeed. In addition to the loss of speed caused by the headwind, there is an additional small loss caused by the fact that you're not pointed the same direction you are going. So, an additional "crab" correction is necessary.    Find the wind correction angle on the black scale to find the "effective true airspeed". To perform this correction, locate the wind correction angle on the small black scale to the left of the "TAS" marker. The value on the outer disk corresponding to this is the "effective true airspeed", which is the component of your true airspeed that is in the direction you want to go. In this example, it's just a bit less than 113kt. (If your wind correction angle is less than about 5°, you can skip this additional step, as the loss due to the crab angle is negligible.) Now you can subtract the headwind from (or add a tailwind to) the effective true airpseed to get ground speed. In our example, we have 113kt - 19kt, giving 94kt. Notice that this is one knot higher than the E6-B solution. The discrepancy is due to inaccuracy in making pencil marks and measurements, combined with accumulated rounding error. The magnitude of this type of error is far less than, for instance, the accuracy of the pilot in flying a precise heading or airspeed, or the accuracy with which the weather conforms to the forecast. A calculation error of 1% or so is insignificant. (Just for the record, the exact answer to five significant figures is 93.397kt, so both 93kt and 94kt are about equally close to "correct".) Which Computer is Better? Once you're comfortable with both types of flight computer, either one gets the job done equally well. The E6-B computer is a little easier to remember how to operate (especially since most models have instructions printed on one end of the slide). On the other hand, the CR computer can be operated with one hand after drawing the wind dot, which is handy when recomputing headings mid-flight. A drawback to most E6-B computers is their size. A typical model is 10" long and 5" wide. The CR-3 on the other hand is just a 6" circle, while the pocket sized CR-5 is just over 4". Being one piece, there's also no danger of the slider falling out in the midst of an in-flight calculation. My personal preference has shifted towards the CR. After working with it for a while, its operation makes as much sense as the E6-B. The small size of the CR-5 lets me keep it in my jacket pocket, so it's always there when I need it. The calculator side is also handy for computing tips, or comparing unit prices of items in the grocery store.     Buy Stefan a coffee! If you've found this article useful, consider leaving a donation to help support stefanv.com   Last updated Friday March 20, 2009. E-mail Stefan   Disclaimer: Although every effort has been made to ensure accuracy and reliability, the information on this web page is presented without warranty of any kind, and Stefan Vorkoetter assumes no liability for direct or consequential damages caused by its use. I am not a flight instructor, aircraft designer, or aircraft mechanic, nor any other professional in this field. I am merely using this site as a medium for sharing my experiences and the things I've learned. It is up to you, the reader, to determine the suitability of, and assume responsibility for, the use of this information. Copyright: All materials on this web site, including the text, images, and HTML mark-up, are Copyright © 2009 by Stefan Vorkoetter unless otherwise noted. All rights reserved. Unauthorized duplication prohibited. You may link to this site or pages within it, but you may not link directly to images on this site, and you may not copy any material from this site to another web site or other publication without express written permission. You may make copies for your own personal use.