The Science of Hammond Organ Drawbar Registration

February 7, 2009

Revised March 2, 2011

When Laurens Hammond introduced the Hammond electric organ to the world in 1934, he gave us an instrument with more control over the sound it produced than any other before it (and many since). The Hammond organ’s drawbars let the player control the nature of the sound at the level of individual harmonics, much like a painter can control the nature of colour by mixing a very few primary colours.

This article is intended to clarify the function of the drawbars, and addresses such issues as combining drawbar settings (for example, how to combine 8′ and 4′ flutes with 8′ strings), and how to create a drawbar setting that most closely matches a particular instrument sound.

A Brief Introduction to the Nature of Sound

Any steady tone has three main attributes: volume, pitch, and timbre (pronounced “tamber”). The first two are pretty much self-explanatory, and won’t be discussed here. The third refers to the quality or character of the tone. Two tones can be of the same volume and pitch but still sound radically different (imagine the same note played on a trumpet and a xylophone).

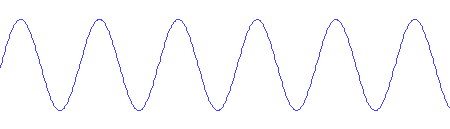
There are several aspects to timbre, one of which is the distribution of harmonics in a tone. Most tones consist of a fundamental, together with several harmonics present in varying degrees. The frequency of the fundamental is what we usually perceive as the tone’s pitch. The purest tone consists of only a fundamental, and looks and sounds like this:

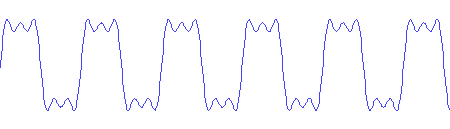
Harmonics are additional pure tones superimposed on the fundamental, each of which has a frequency that is an integer multiple of the fundamental. Instead of hearing the harmonics as distinct tones, our ears and brain hear a tone of the fundamental frequency, but with a different character than the pure tone. For example, here is a tone with the same pitch as the sample above, but consisting of the fundamental with a bit of the third harmonic (3x the fundamental frequency) and a bit less of the fifth harmonic (5x the fundamental frequency) thrown in:

Notice that the tone still has the same pitch, but that the character of the sound is very different.

The Hammond drawbars give the player control over the combination of fundamental and harmonic frequencies. There are nine drawbars for setting the levels of the fundamental and various harmonics and sub-harmonics (lower in frequency than the fundamental).

Each drawbar has nine positions labelled from 0 to 8. Zero means off; the harmonic controlled by that drawbar will not appear in the generated tones. The remaining positions will cause the specified harmonic to appear in varying amounts, with each increment producing about a 3dB increase.

As a convenient shorthand, drawbar settings are usually written as a sequence of nine digits broken into groups of two, four, and three digits respectively. For example, a possible drawbar setting sounding like an 8′ Tibia stop is 00 8040 000.

Drawbar Settings as (Pipe Organ) Stops

The individual drawbars are believed by some to be the equivalent of stops on a pipe organ, but they should not be seen this way. When an organist selects a single stop on a pipe organ, the resulting tone will be a complex one with many harmonics. The complexity of the tone depends on the type and number of ranks of pipes that the stop controls. A stop controlling a single rank of flute pipe will produce almost pure tones, whereas one controlling two ranks of diapason pipes will produce tones rich in harmonics.

Hammond drawbars on the other hand select individual harmonics. Usually several drawbars must be pulled varying amounts to achieve the effect of an individual stop.

For any given stop found on a typical church or theatre pipe organ, there will be a drawbar setting that approximates the sound of that stop on a Hammond organ. Sometimes the imitation will be almost perfect (when all the harmonics produced by the pipe stop are also ones available via the drawbars), and sometimes less so (such as a stop that contains a significant amount of 7th harmonic).

Here are some typical pipe organ stops, along with possible Hammond drawbar registrations to imitate those stops, and an audio clip of each:

Stop	Drawbar Setting	Sample
Bass Violin 16′	14 5431 000	Listen
Tibia 8′	00 8040 000	Listen
Bassoon 8′	07 8120 000	Listen
French Trumpet 8′	00 7888 872	Listen

Drawbar Settings as Registrations

More often than not when playing a church or theatre pipe organ, several stops will be selected at once, causing pipes from multiple ranks to sound when a key is pressed. Some stops are quite boring when played in isolation, so other stops are added to change the character of the resulting sound.

Such a collection of stops to produce a desired sound is called a registration. Registrations can be set up manually by pulling the desired stops, or by means of pre-programmed combination pistons which can activate a handful of stops at once.

If a drawbar setting can be considered equivalent to a stop, how does one create an entire registration? The answer lies in combining two or more drawbar settings into a new drawbar setting that combines the characteristics of all the desired stops. So like a simple stop, an entire registration is also a drawbar setting. The best way to combine the settings for multiple stops into a single setting for a registration is the subject of the next section.

First, here are some registrations consisting of combinations of some of the stops from the previous section, with drawbar settings and audio clips:

Registration	Drawbar Setting	Sample
Bass Violin 16′ and Tibia 8′	14 8451 000	Listen
Bassoon 8′ and French Trumpet 8′	06 8777 761	Listen

Combining Drawbar Settings

There are several schools of thought on how drawbar settings for stops should be combined to produce a registration. Mathematical analysis based on the physics of sound and the workings of the Hammond organ show some of them to be misconceived.

The first is from the Dictionary of Hammond Organ Stops, in which Stevens Irwin suggests:

The method is to add the drawbar-indications for each drawbar pitch, using the figure 8 if the sum comes to above 8.

I find two serious flaws with this method:

• This method doesn’t take into account the fact that the drawbar values are logarithmic (since each increment represents 3dB, and the dB scale is logarithmic).

• Setting all sums greater than 8 to be just 8 is inconsistent. Following this rule means that 8+1 and 8+8 both give 8, whereas the latter should clearly be louder. Furthemore, adding too many drawbar settings together will always yield 88 8888 888.

Irwin then writes:

Porter Heaps suggests taking the largest figure for each harmonic drawbar in the group of stops to be combined as the proper intensity for the final ensemble.

In Hammond Organ Additive Synthesis – A New Method, Paul Schnellbecher responds,

I couldn’t accept the idea that combining two powerful stops and a medium string could be simulated by using the most powerful stop with only a tiny contribution from the string.

Schnellbecher then proposes that a more sensible way is to just add the stops together, and then if at the end of this process any drawbar setting is higher than 8, divide each drawbar setting by 2 as many times as necessary until this is no longer the case. Although I agree with Schnellbecher’s sentiments above, this suffers from the same flaw (not considering the logarithmic nature of the drawbar settings) as Irwin’s suggestion. Furthermore, why divide by 2? Why not 1½ or π? It would make more sense to divide by the highest setting and then multiply by 8, thus giving the loudest drawbar a setting of 8.

A Mathematically Sound Approach

The method I’m about to propose adheres to the following principle:

A combination of two drawbar settings should sound as much as possible as if the two settings were played at the same time on separate Hammond organs (or recorded separately and then mixed).

Let’s first look at combining the settings for a single drawbar, say the first white drawbar (8′). For example, suppose that both stops we’re interested in combining have that drawbar set to 5. It stands to reason that in the resulting registration, the contribution of the 8′ drawbar should have twice the power (√2 times the volume) that it has in either stop alone. After all, playing the same thing on two organs produces twice the output power as playing it on one.

Recall that each drawbar increment corresponds to a 3dB volume increase. That happens to be √2 times the volume, and thus twice the power. Therefore, the resulting setting for the 8′ drawbar should be 6. In drawbar setting numbers, 5 + 5 = 6. Similarly, 1 + 1 = 2, 2 + 2 = 3, 3 + 3 = 4, 4 + 4 = 5, 5 + 5 = 6, 6 + 6 = 7, 7 + 7 = 8, and 8 + 8 = 9. In other words, whenever combining two equal settings, the result is one increment higher than that setting.

What about unequal values? The trick is to convert from drawbar setting numbers to linear power figures, add those together, and convert the sum back to a drawbar number. The following table gives the correspondence:

Drawbar Setting	Linear Power	Power Range
0	0	0.000 – 0.706
1	1	0.707 – 1.413
2	2	1.414 – 2.827
3	4	2.828 – 5.656
4	8	5.657 – 11.30
5	16	11.31 – 22.62
6	32	22.63 – 45.24
7	64	45.25 – 90.50
8	128	90.51 – 181.0

For example, to add drawbar settings of 4 and 7, add the corresponding linear powers, giving 8 + 64 = 72. The result is still within the linear power range of setting number 7, so the resulting setting should be 7. Let’s try combining 3 and 4. Adding the linear powers gives 12, which is within the range of setting 5.

What happens if we add 8 and 7? The resulting linear power is 192, which is above the highest available. In cases where the linear power is greater than 181 (which corresponds to a drawbar setting of just under 8.5) we first have to finish adding the linear powers of the other drawbars, then divide all the sums by the largest and multiply by 181. The resulting set of linear powers can then be converted back to drawbar settings.

This procedure can be expanded to as many separate settings as you wish to combine into one. Convert all the settings to linear powers, add up the corresponding powers, divide by the largest and multiply by 181 if necessary, and convert the results back to drawbar settings.

A Drawbar Combination Calculator

To make it easy to use the method described above, I’ve created an on-line drawbar calculator. Enter as many drawbar settings as you’d like to combine, one per line into the input area below, and click the Combine button:

A Note to the Mathematically Inclined: The formula used to convert a drawbar setting of n to linear power is 2^(n-1), the exception being the zero setting. Why is there an exception? Because the all-the-way-in position of the drawbar should really be labelled negative infinity. Zero dB is not silence.

Comparing the Methods

Consider combining the drawbar settings 00 7656 010 (an 8′ Open Diapason) and 00 0402 010 (4′ Octave) using each of the four methods:

• 00 7656 010 + 00 0402 010 = 00 7858 020 (Irwin)
• 00 7656 010 + 00 0402 010 = 00 7656 010 (Heaps)
• 00 7656 010 + 00 0402 010 = 00 4534 010 (Schnellbecher)
• 00 7656 010 + 00 0402 010 = 00 7656 020 (My Method)

The four methods produce very different results. In Irwin’s method, the fourth and sixth drawbars (2nd and 4th harmonics) are too loud. In Heaps’ method, the combined setting is the same as the first setting, as if the second had been ignored. Schnellbecher’s method results in a combination that is quieter than either of its parts.

Using my method, the highest setting is only 7 because none of the sums result in a power greater than a setting of 7 would. Also notice the eighth drawbar (the 6th harmonic), where my method correctly accounts for the doubling of power resulting from adding two settings of 1.

The differences between the methods are even more striking when combining more than two settings. For example, consider combining these four settings: 00 1565 653 (8′ Violin), 00 0113 064 (4′ Violina), 00 8040 000 (8′ Tibia), and 00 0800 030 (4′ Tibia). The results using each of the methods are:

• 00 8888 687 (Irwin)
• 00 8865 664 (Heaps)
• 00 5764 374 (Schnellbecher)
• 00 8865 675 (My Method)

The Irwin method produces a setting that is almost straight 8’s, thus no longer reflecting the character of any of the individual voices. Once again, Schnellbecher’s method gives a much quieter result than all the rest.

You will notice that there is often little difference between my method and that of Porter Heaps. In fact, when combining only two drawbar settings, my method and Heaps’ will differ only if corresponding drawbars are within one increment of each other in the two settings, and will differ by only one increment in the result (for example, 4 + 4 gives 5 with my method, and 4 with Heaps’ method). When combining more than two settings, the methods can diverge further, although in the four-voice example above, they still only differ by at most one.

This is the Second Revision of My Method

When I originally wrote this article in early 2009, I used the same principle as above, except that I linearly combined volume, not power. In hindsight, this was a mistake. Two organs playing the same sound will not be twice as loud, but will produce twice the power. The revision of the article you are now reading, made in March 2011, correctly combines power.

Reducing the Volume of a Drawbar Setting

In order to achieve a desired balance between the upper and lower manuals when playing a piece of music, it is often necessary to reduce the volume of a drawbar setting (for instance, to make the accompaniment quiet enough that the melody can be clearly heard). The technique to reduce the volume is trivial: push each drawbar in by the same amount.

For example, the following settings all produce the same sound but at increasingly lower levels:

00 8767 054

00 7656 043

00 6545 032

00 5434 021

Once the setting contains a “1” somewhere within it, any further reductions will affect the character of the sound. Moving a drawbar from a setting of 8 to 7 or from 2 to 1 reduces the contribution of that drawbar by 3dB, but moving it from 1 to 0 turns it off completely (i.e. reduces it by an infinite number of decibels).

Finding the Drawbar Setting to Match a Sound

So far we’ve looked at how to combine drawbar settings representing one or more stops to create a setting for a registration. The other part of the puzzle is how to find a drawbar setting to match a particular pipe organ stop or other musical instrument in the first place.

The traditional method is of course by ear. With experience, a Hammond organist learns how the relative settings of the drawbars affect the character of the sound produced. However, it takes a while to gain that experience, and in this era of instant gratification, there is an easier way!

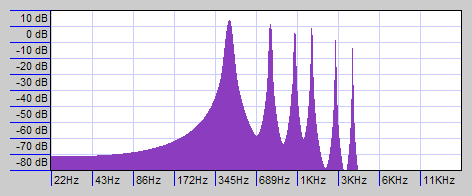
As we’ve discussed, the drawbars control the relative volume of the harmonics of the sounds produced. This distribution of harmonics is visible when one plots the frequency spectrum of the sound. For example, here is the spectrum of a 440Hz tone played with registration 00 8767 054:

The peaks and their amplitudes are:

Frequency	Harmonic	Amplitude	Relative Amplitude	Drawbar Setting
440 Hz	Fundamental	4dB	0dB	8
880 Hz	2nd	1dB	-3dB	7
1320 Hz	3rd	-2dB	-6dB	6
1760 Hz	4th	1dB	-3dB	7
2200 Hz	5th	-88dB	-92dB	0
2640 Hz	6th	-5dB	-9dB	5
3520 Hz	8th	-8dB	-12dB	4

If we now arbitrarily equate 0dB to a drawbar setting of 8, then every 3dB down from that corresponds to one drawbar increment down (anything -24dB or below becomes zero). One can see that the frequency spectrum of the tone corresponds exactly to the drawbar setting that produced it.

One can take advantage of this to derive a drawbar setting for an arbitrary tone. Starting with a recorded sample of the tone, use a tool like Audacity to generate a spectrum analysis, and write down the intensity of each peak. Equate the highest intensity to a setting of 8 and determine the settings of the remaining drawbars relative to that, so that each 3dB down from the highest corresponds to one drawbar increment down.

This technique works for almost any steady tone that one can get a recording of. For example, I found this short clip on www.freesound.org of a female vocalist singing melisma style. Here is the frequency spectrum from the second G# note in the performance:

The peaks and their amplitudes, and the corresponding drawbar settings, are:

Frequency	Harmonic	Amplitude	Relative Amplitude	Drawbar Setting
415 Hz	Fundamental	9dB	-2dB	7
831 Hz	2nd	11dB	0dB	8
1246 Hz	3rd	0dB	-11dB	4
1661 Hz	4th	-5dB	-16dB	3
2077 Hz	5th	-19dB	-30dB	0
2492 Hz	6th	-31dB	-42dB	0
3322 Hz	8th	-18dB	-29dB	0

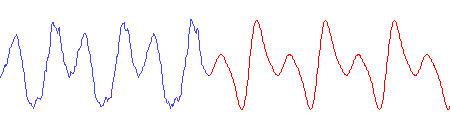
The drawbar setting to match this singer’s voice as closely as possible is thus 00 7843 000. Here is a clip of the aforementioned G# as sung by the vocalist, followed by the same note played with this drawbar setting:

The graphic above shows both the singer’s waveform (blue), and the Hammond’s (red). The shapes aren’t exactly the same because the phase relationship between the harmonics isn’t the same, but research has shown that our hearing is insensitive to phase relationship. Also notice that in the singer’s waveform, there are additional small “jaggies”. These are from the higher harmonics that the Hammond cannot produce.

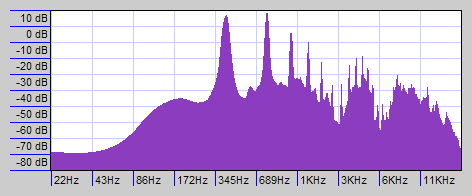
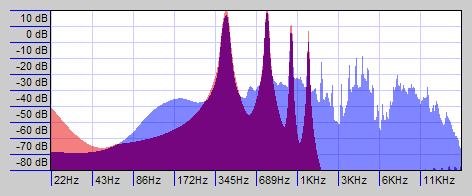
Here is another spectrum plot, comparing the spectra of the vocalist with that of the Hammond imitation. The purple areas are where the spectra coincide. Notice that all the higher harmonics are missing from the Hammond tone, as is all the non-harmonic content of the actual singer’s voice:

Hammond Shortcomings

Although a Hammond organ can reproduce many pipe organ stops, pipe organ registrations, and arbitrary sounds quite well, it falls short in some respects. Some of the shortcomings are:

• If you create a drawbar setting for a pipe organ stop, it can often sound very much like the real thing. But if you create a setting for a combination of stops (a registration), it may not sound as full as the actual organ. When multiple ranks of pipes play at once, they will never be perfectly in tune with one another. On the Hammond however, the harmonics for all the stops are being produced by the same tonewheels, so it will sound as if the pipes were exactly in tune. The result might be too perfect to sound realistic.

• The Hammond drawbars only give you up to the 8th harmonic, omitting the 7th. Sounds that contain significant portions of 7th harmonic or harmonics beyond the 8th will be lacking when reproduced on the Hammond. Additional harmonics are available on some models. For example, the spinet models provide a combined 10th/12th harmonic drawbar on the lower manual, and the H-100 series provide both 7th/9th and 10th/12th drawbars.

• When more than one note is played, the same tonewheel might be contributing different harmonics to different notes. In theory, that tonewheel’s contribution will sound proportionally louder, but in practice, it will not be quite as loud as expected due to resistive losses in the magnetic pickup.

• There’s more to timbre than the character of the tone. The envelope is also important. For example, a Hammond organ can be set to play approximately the same harmonics as a piano, but it will never sound like a piano. Piano notes have a sudden but not instantaneous attack followed by a gradual decay. Hammond notes have a nearly instantaneous attack (complete with key click), followed by steady volume, followed by an instantaneous decay.

References

Dictionary of Hammond Organ Stops – A Translation of Pipe Organ Stops Into Hammond-Organ Number Arrangements, by Stevens Irwin, 1939, 1952, 1961, and 1970.

A Primer of Organ Registration, by Gordon Balch Nevin, 1920. A copy of this book is available on-line at Scribd.com.

A Case Study: Tonewheels, by John Savard, 2010, 2012. This page goes into the workings of Hammond tonewheels in great detail, and is highly recommended reading for the technically inclined Hammond enthusiast.

                    

Related Articles

If you've found this article useful, you may also be interested in:

• On the Nature of “The Hammond Organ Sound”