Op-Amp Oscillator Design with the HP-67 Programmable Calculator
November 26, 2008
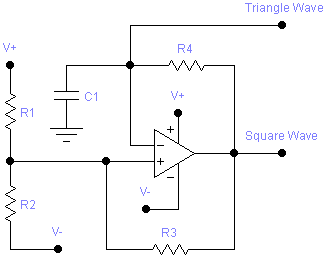
This is my second HP-67 program, which I wrote to help me with the design of a project that is currently (Nov. 2008) in the planning stages. This program selects component values for an op-amp based relaxation oscillator, given the desired frequency and output wave form peak voltages. It can also solve the inverse problem, finding the frequency and voltages resulting from given component values. The following is the schematic for such an oscillator:
R1 and R2 form a voltage divider, with an additional input from the op-amp output through R3. When the op-amp output is at a high-level, the voltage at the non-inverting input of the op-amp is higher than when the op-amp output is at a low level. When the output is high, capacitor C1 also charges through R4 until the voltage across it (which is applied to the op-amp’s inverting input) reaches the voltage at the non-inverting input. At that time, the op-amp output goes low, and the capacitor begins to discharge through R4 until the voltage once again reaches the (now lower) voltage at the non-inverting input.
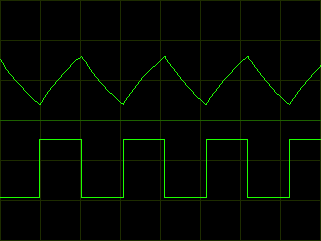
If one were to monitor the op-amp output, it would alternate between a high level (VOH, generally close to positive supply voltage, VPOS) and a low level (VOL, generally close to negative supply voltage, VNEG). The duty cycle of this square wave depends on the relative time it takes to charge and discharge C1 through R4, which in turn depends on the low (VPL) and high (VPH) peak voltages that C1 cycles between (which in turn depend on R1, R2, and R3). Monitoring the voltage across C1 shows a triangle wave.
With this program, you can select components for such an oscillator to achieve a desired frequency, and if it matters to your design, desired low and high triangle peaks (VPL and VPH). After the program computes the required component values, you can modify these values to match those actually available in the real world. The program will then compute what effect these changes have on the frequency and triangle peak voltages.
The following equations describe the operation of the oscillator:
You will first need to choose values for C1 and R1 arbitrarily, since for any desired frequency and given C1 and R1, it will be possible to find (possibly impractical) values for R2, R3, and R4. A good choice for R1 is generally somewhere around 10kΩ to 100kΩ. The choice of C1 depends on the frequency, and a readily available value near (50/f) μF is usually suitable.
Using the Program
First type in the program and save it, or read it from a previously recorded magnetic card. The card should be labelled as follows:
| OP-AMP OSCILLATOR DESIGN | ||||
|---|---|---|---|---|
| VNEG,VPOS | VOL,VOH | C1 | R1 | VPL,VPH |
| f | →%DC | →R2→ | →R3→ | →R4→ |
Forward Solution: Finding R2, R3, and R4
Consider the following example: It is desired to find values for R2, R3, and R4 to produce an oscillator of about 2500Hz, with a triangle waveform that oscillates between 1.2V and 1.4V. The op-amp is to operate from a single 5V supply, and the op-amp’s output is capable of a low of 0.3V and a high of 5V. Use a 0.022μF capacitor for C1, and a 22kΩ resistor for R1.
Follow these steps to solve the problem:
| Description | Keystrokes | Display |
|---|---|---|
| Select engineering notation | h ENG DSP 2 |
0.00 00 |
| Enter power supply voltages | 0 ENTER 5 f a |
0.00 00 |
| Enter low and high level output voltages | 0.3 ENTER 5 f b |
300. -03 |
| Enter C1 (Farads) | 0.022 EEx CHS 6 f c |
22.0 -09 |
| Enter R1 (Ohms) | 22 EEx 3 f d |
22.0 03 |
| Enter desired triangle lower and upper voltage peaks | 1.2 ENTER 1.4 f e |
1.20 00 |
| Enter desired frequency (Hz) | 2500 A |
2.50 03 |
| Compute square wave duty cycle | B | 788. -03 |
| Compute value of R2 (Ohms) | C | 7.26 03 |
| Compute value of R3 (Ohms) | D | 123. 03 |
| Compute value of R4 (Ohms) | E | 71.4 03 |
Notes
Specifying VOL and VOH is optional. If this step is omitted, the program will assume the op-amp output can span the entire negative and positive supply voltage range.
If the triangle wave form peak voltages don’t matter to your design (because you’re only using the square wave output), you don’t need to specify them. The program will assume peak voltages ranging from VOL+(VOH–VOL)/3 to VOH-(VOH–VOL)/3, which is the middle third of the op-amp output voltage range. This also happens to result in a 50% duty cycle.
To achive a low duty cycle square wave, choose VPL and VPH close to the bottom of the op-amp output range (VOL). Likewise for a high duty cycle, choose VPL and VPH close to the top of the range (VOH).
For the most stable oscillation frequency, choose VPL and VPH far away from the op-amp output voltage limits, VOL and VOH (to keep the triangle edges steep), and far away from each other (to keep any variations a small percentage of the overall voltage swing). Since these two goals are at odds with one another, a good compromise is to select VPL and VPH to span the middle of the VOL to VOH range (which is the default if VPL and VPH aren’t specified).
Reverse Solution: Finding VPL, VPH, Frequency, and Duty Cycle
After finding the above ideal solution, we’ll want to use real-world component values to build the physical circuit. The closest E-24 resistor values to those computed are: R2 = 7.5kΩ, R3 = 120kΩ, and R4 = 68kΩ. What effect will using these values have on the frequency, VPL, and VPH?
These are the steps to find out:
| Description | Keystrokes | Display |
|---|---|---|
| Enter new value for R2 | 7.5 EEx 3 C |
7.50 03 |
| Enter new value for R3 | 120 EEx 3 D |
120. 03 |
| Enter new value for R4 | 68 EEx 3 E |
68.0 03 |
| Compute resulting value for VPL | f e | 1.23 00 |
| Compute resulting value for VPH | R/S | 1.44 00 |
| Compute resulting frequency | A | 2.57 03 |
Other Uses for this Program
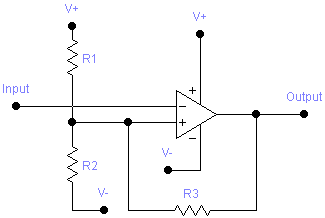
The oscillator design facilitated by this program consists of two parts, a comparator with hysteresis, and a capacitor being charged and discharged by the comparator output through a resistor. The equations describing the comparator aspect of the circuit are not affected by those describing the behaviour of the resistor-capacitor network, so the program can be used to design such comparators for other applications.
Here is a brief example of using this program to design a comparator: Assume we want to design a comparator operating from a +/-12V supply, whose output goes low when the voltage exceeds +2V, and goes high when the voltage subsequently drops below -3V. Assume the op amp used has an output that can swing to within 0.7V of the voltage limits. Use a 10kΩ resistor for R1. Follow these steps to solve the problem:
| Description | Keystrokes | Display |
|---|---|---|
| Enter power supply voltages | 12 CHS ENTER 12 f a |
-12.0 00 |
| Enter low and high level output voltages | 11.3 CHS ENTER 11.3 f b |
-11.3 00 |
| Enter R1 | 10 EEx 3 f d |
10.0 03 |
| Enter desired lower and upper switching points | 3 CHS ENTER 2 f e |
-3.00 00 |
| Compute value of R2 | C | 8.98 03 |
| Compute value of R3 | D | 16.7 03 |
Now select the closest real-world resistor values for R2 and R3 and determine how that affects the switching points:
| Description | Keystrokes | Display |
|---|---|---|
| Enter new value for R2 | 9.1 EEx 3 C |
9.10 03 |
| Enter new value for R3 | 16 EEx 3 D |
16.0 03 |
| Compute resulting lower switching point | f e | -3.03 00 |
| Compute resulting upper switching point | R/S | 2.16 00 |
Additional Real-World Considerations
The mathematical model used as the basis of this program assumes that VOL and VOH are constant, regardless of load. For sufficiently low current, this is close enough to true to be ignored. Thus it is important to use fairly high resistor values for R3 and R4 (10kΩ or bigger to be on the safe side). If the value of R3 computed by the program is too low, start with a higher value for R1. Similarly, if the value computed for R4 is too low, use a lower value for C1.
Some op-amps have an open-collector output. This means that when the output is low, it is pulled low through an output transistor, but when the output is high, it is simply floating. Thus, a pull-up resistor is needed to pull the output high. The chosen pull-up resistor must meet two requirements:
-
It must have a high-enough resistance that the output transistor can overcome the pull-up current when the output is low.
-
It must have a low-enough resistance that it is not so large a percentage of the resistance of R3 or R4 that it throws off the solution.
For the LM339 comparator that I often use in my designs, I’ve found that a 1kΩ resistor works well, together with R3 and R4 values about 100 times as much. As described above, use a higher value for R1 to achieve a higher value for R3, and use a lower value for C1 to achieve a higher R4.
Program Listing
| Line | Instruction | Comments |
|---|---|---|
| 001♦ | LBL a | Store VNEG and VPOS |
| 002 | STO 6 | VPOS |
| 003 | x↔y | |
| 004 | STO 5 | VNEG |
| 005 | x↔y | Fall through and initialize VOL and VOH to VNEG and VPOS |
| 006♦ | LBL b | Store VOL and VOH |
| 007 | CF 3 | |
| 008 | STO 8 | VOH |
| 009 | x↔y | |
| 010 | STO 7 | VOL |
| 011 | − | Initialize VPL and VPH |
| 012 | 3 | |
| 013 | ÷ | (VOH–VOL)/3 |
| 014 | RCL 7 | |
| 015 | x↔y | |
| 016 | + | |
| 017 | STO A | Set VPL = VOL + (VOH–VOL)/3 |
| 018 | RCL 8 | |
| 019 | LSTx | |
| 020 | − | |
| 021 | STO B | Set VPH = VOH – (VOH–VOL)/3 |
| 022 | CF 1 | |
| 023 | RCL 8 | Leave VOL and VPH on stack as feedback to user |
| 024 | RCL 7 | |
| 025 | RTN | |
| 026♦ | LBL c | Store C1 |
| 027 | CF 3 | |
| 028 | STO C | |
| 029 | RTN | |
| 030♦ | LBL d | Store R1 |
| 031 | CF 3 | |
| 032 | STO 1 | |
| 033 | RTN | |
| 034♦ | LBL e | Store or compute (if necessary) VPL and VPH |
| 035 | F? 3 | If data entered, store new VPL and VPH |
| 036 | GTO 9 | |
| 037♦ | LBL 1 | Otherwise, compute VPL and VPH if necessary |
| 038 | F? 1 | Need to compute VPL and VPH? |
| 039 | GTO 8 | |
| 040 | RCL B | Recall already-up-to-date VPL and VPH |
| 041 | RCL A | |
| 042 | RTN | |
| 043 | RCL B | If user presses R/S after seeing VPL, display VPH |
| 044 | RTN | |
| 045♦ | LBL 8 | Recompute VPL and VPH |
| 046 | RCL 1 | |
| 047 | RCL 3 | |
| 048 | × | |
| 049 | STO D | |
| 050 | RCL 2 | |
| 051 | RCL 3 | |
| 052 | × | |
| 053 | ST I | |
| 054 | + | |
| 055 | RCL 2 | |
| 056 | RCL 1 | |
| 057 | × | |
| 058 | STO 9 | |
| 059 | + | |
| 060 | 1/x | |
| 061 | STO E | |
| 062 | RCL 5 | |
| 063 | × | |
| 064 | RCL D | |
| 065 | × | |
| 066 | RCL E | |
| 067 | RCL 6 | |
| 068 | × | |
| 069 | RC I | |
| 070 | × | |
| 071 | + | |
| 072 | STO D | Partial result common to VPL and VPH |
| 073 | RCL E | |
| 074 | RCL 9 | |
| 075 | × | |
| 076 | STO E | End of computation common to VPL and VPH |
| 077 | RCL 7 | Compute VPL |
| 078 | × | |
| 079 | + | End of computation of VPL |
| 080 | RCL E | Compute VPH |
| 081 | RCL 8 | |
| 082 | × | |
| 083 | RCL D | |
| 084 | + | End of computation of VPH; VPL is in Y-register |
| 085♦ | LBL 9 | Store entered or computed VPH and VPL |
| 086 | STO B | Store VPH |
| 087 | x↔y | |
| 088 | STO A | Store VPL |
| 089 | CF 1 | VPL and VPH are now up to date |
| 090 | RTN | |
| 091 | RCL B | If user presses R/S after seeing VPL, display VPH |
| 092 | RTN | |
| 093♦ | LBL B | Compute duty cycle |
| 094 | CF 3 | |
| 095 | GSB 7 | Get numerator and denominator (also used for computing R4 or f) |
| 096 | LSTx | Numerator |
| 097 | x↔y | |
| 098 | ÷ | |
| 099 | RTN | |
| 100♦ | LBL 7 | Compute denominator of duty cycle, leaving numerator in LSTx |
| 101 | GSB 1 | Recompute VPL and VPH if necessary; leaves VPH in X, VPL in Y |
| 102 | RCL 8 | Compute first half of denominator |
| 103 | − | |
| 104 | RCL B | |
| 105 | RCL 8 | |
| 106 | − | |
| 107 | ÷ | |
| 108 | LN | |
| 109 | RCL B | Compute second half of denominator (which is also the numerator) |
| 110 | RCL 7 | |
| 111 | − | |
| 112 | RCL A | |
| 113 | RCL 7 | |
| 114 | − | |
| 115 | ÷ | |
| 116 | LN | |
| 117 | + | Combine two halves, leaving numerator in LSTx |
| 118 | RTN | |
| 119♦ | LBL A | Store or compute f |
| 120 | F? 3 | |
| 121 | GTO 0 | |
| 122 | GSB 7 | Get denominator (also used for computing R4 and duty cycle) |
| 123 | RCL 4 | Multiply by R4 and C1 |
| 124 | × | |
| 125 | RCL C | |
| 126 | × | |
| 127 | 1/x | |
| 128♦ | LBL 0 | Store entered or computed f |
| 129 | STO 0 | |
| 130 | RTN | |
| 131♦ | LBL C | Store or compute R2 |
| 132 | F? 3 | |
| 133 | GTO 2 | |
| 134 | GSB 5 | Compute numerator of R2 |
| 135 | RCL 6 | Compute denominator of R2 |
| 136 | GSB 6 | |
| 137 | ÷ | |
| 138 | STO 2 | Store computed R2 |
| 139 | RTN | |
| 140♦ | LBL 2 | Store R2 and invalidate VPL and VPH |
| 141 | STO 2 | |
| 142 | SF 1 | Must recompute VPL and VPH for user-defined R2 |
| 143 | RTN | |
| 144♦ | LBL D | Store or compute R3 |
| 145 | F? 3 | |
| 146 | GTO 3 | |
| 147 | GSB 5 | Compute numerator of R3 (same as R2) |
| 148 | RCL 6 | Compute denominator of R3 |
| 149 | RCL 5 | |
| 150 | − | |
| 151 | ÷ | |
| 152 | RCL A | |
| 153 | RCL B | |
| 154 | − | |
| 155 | ÷ | |
| 156 | STO 3 | Store computed R3 |
| 157 | RTN | |
| 158♦ | LBL 3 | Store R3 and invalidate VPLh and VPH |
| 159 | STO 3 | |
| 160 | SF 1 | Must recompute VPL and VPH for user-defined R3 |
| 161 | RTN | |
| 162♦ | LBL E | Store or compute R4 |
| 163 | F? 3 | |
| 164 | GTO 4 | |
| 165 | GSB 7 | Get denominator (also used for computing f or duty cycle) |
| 166 | RCL 0 | |
| 167 | × | |
| 168 | RCL C | |
| 169 | × | |
| 170 | 1/x | |
| 171♦ | LBL 4 | Store entered or computed R4 |
| 172 | STO 4 | |
| 173 | RTN | |
| 174♦ | LBL 5 | Compute numerator common to R2 and R3 |
| 175 | GSB 1 | Recompute VPL and VPH if necessary |
| 176 | RCL 5 | |
| 177 | GSB 6 | |
| 178 | RCL 1 | |
| 179 | × | |
| 180 | CHS | |
| 181 | RTN | |
| 182♦ | LBL 6 | Compute (VOL – VPL – VOH + VPH) * X + VOH * VPL – VPH * VOL |
| 183 | RCL 7 | |
| 184 | RCL A | |
| 185 | − | |
| 186 | RCL 8 | |
| 187 | − | |
| 188 | RCL B | |
| 189 | + | |
| 190 | × | Multiply (VOL – VPL – VOH + VPH) by VPOS or VNEG (now in Y) |
| 191 | RCL 8 | |
| 192 | RCL A | |
| 193 | × | |
| 194 | + | |
| 195 | RCL B | |
| 196 | RCL 7 | |
| 197 | × | |
| 198 | − | |
| 199 | RTN |
Registers and Flags
| Register | Use |
|---|---|
| 0 | Frequency (Hz) |
| 1,2,3,4 | Resistors R1, R2, R3, and R4 (Ohms) |
| 5,6 | VNEG and VPOS (Volts) |
| 7,8 | VOL and VOH (Volts) |
| A,B | VPL and VPH (Volts) |
| C | Capacitor C1 (Farads) |
| 9,D,E,I | Temporary registers |
| Flag | Meaning |
|---|---|
| 1 | VPL and VPH need to be recomputed |
| 3 | User supplied input |
Revision History
2008-Nov-26 — Initial release.
2009-May-25 — Fixed a bug that caused an error if one did not specify VPL and VPH. Changing R1 no longer forces VPL and VPH to be recomputed.
2009-Jun-11 — Fixed a bug where the data entry flag sometimes wasn’t cleared even though there had been no data entry.
2015-Jun-23 — Fixed a bug in the subroutine for computing the denominator of the duty cycle, wherein VPL and VPH were accidentally interchanged. Bug was in web-site listing only, not in original program.
Related Articles
If you've found this article useful, you may also be interested in:
- Op-Amp Gain and Offset Design with the HP-41C Programmable Calculator
- Op-Amp Oscillator Design with the HP-41C Programmable Calculator
- Low-Sensitivity Sallen-Key Filter Design with the HP-41C Programmable Calculator
- Low-Sensitivity Sallen-Key Filter Design with the HP-67 Programmable Calculator
- Op-Amp Gain and Offset Design with the HP-67 Programmable Calculator
- Resistor Network Solver for the HP-67 Programmable Calculator
- A Matrix Multi-Tool for the HP 35s Programmable Calculator
- Curve Fitting for the HP 35s Programmable Calculator

If you've found this article useful, consider leaving a donation in Stefan's memory to help support stefanv.com
Disclaimer: Although every effort has been made to ensure accuracy and reliability, the information on this web page is presented without warranty of any kind, and Stefan Vorkoetter assumes no liability for direct or consequential damages caused by its use. It is up to you, the reader, to determine the suitability of, and assume responsibility for, the use of this information. Links to Amazon.com merchandise are provided in association with Amazon.com. Links to eBay searches are provided in association with the eBay partner network.
Copyright: All materials on this web site, including the text, images, and mark-up, are Copyright © 2025 by Stefan Vorkoetter unless otherwise noted. All rights reserved. Unauthorized duplication prohibited. You may link to this site or pages within it, but you may not link directly to images on this site, and you may not copy any material from this site to another web site or other publication without express written permission. You may make copies for your own personal use.
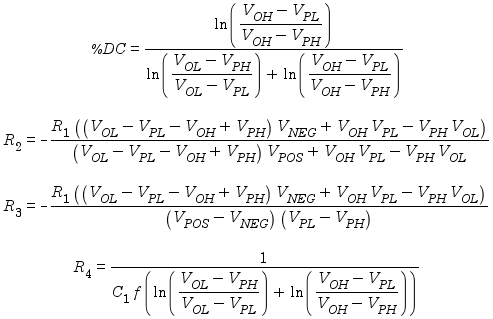
Willy Kunz
May 16, 2013
The program as shown in the listing gives wrong answers for duty cycle and resistor R4. To fix it:
Step 109: change RCL A to RCL B
Step 112: change RCL B to RCL A
Step 116: insert x↔y after LN
With these changes, the duty cycle is shown as 212.-03 which is equivalent to 788.-03 (=1-0.212).