Curve Fitting for the HP 35s Programmable Calculator

October 17, 2007

The 2007 retro HP 35s programmable calculator.

The 2007 retro HP 35s programmable calculator.

Hewlett-Packard’s new-for-2007 HP 35s programmable scientific calculator isn’t historical yet, but it has the HP quality, look, and feel that has been missing for over a decade. The 35s is more like HP’s historical offerings than it is like their other current products, which is a good thing. Since I used to enjoy programming calculators when I was younger and hadn’t done so in years, I decided to tackle some largish (for a calculator) programs on my brand new HP 35s. In addition to this curve fitting program, I’ve written a matrix multi-tool.

Both the HP-41C/CV/CX Advantage Pac and the HP-42S calculator contain a curve fitting function which can fit a sequence of (x,y) data pairs to a straight line, logarithmic, exponential, or power curve. The much newer HP 35s will only fit points to a straight line. The manual provides a program to handle the other curve types, but that program has two drawbacks: you must decide in advance which curve you want to fit to the data, and it uses up a large number of labels (the machine has only 26).

The program presented below rectifies both of these issues. It uses only a single label, and it allows you to fit multiple curves to the same data set. Like the HP-41/42 programs, it also has a best-fit mode wherein it automatically chooses the curve with the best correlation coefficient. The available curves are:

Linear:

y = m x + b

Logarithmic:

y = m ln x + b

Exponential:

y = b em x

Power:

y = b xm

The logarithmic and power curves require that all the x values be positive. Similarly, the exponential and power curves require that all the y values be positive. After choosing a curve to fit, or having the program choose one for you, you can predict values of y for given x values, or vice versa.

Using the Program

This program is integrated as closely as possible with the HP35s’ built-in statistical registers and functions. Before entering a new data set, clear the statistics registers by pressing blue shift CLEAR 4Σ.

Then press XEQ C ENTER to run the curve fitting program. This will display the main menu, which looks like this:

The menu choices are:

  1. Go to data entry mode.
  2. Delete the last data pair entered.
  3. Go to the curve fitting menu.
  4. Compute x given a y value.
  5. Compute y given an x value.

Pressing R/S without selecting a choice exits the curve fitting program (this is important, to ensure flag 10 is cleared so equations will work in other programs).

Data Entry Mode

Press 1 R/S to go to data entry mode. The X-register of the display will show the number of points entered so far (which will be zero if you had just cleared the statistics registers). To enter a data pair, first enter the y value, press ENTER, enter the x value, and press R/S. The program will briefly display RUNNING, and then display the updated number of points (the Y-register will contain the y value just entered).

When you’ve completed data entry, press XEQ C ENTER to return to the main menu.

Deleting the Last Entry

If you’ve made a mistake entering a data pair, here’s how to correct it:

  • If you haven’t pressed R/S yet, just enter the correct data pair and then press R/S.
  • If you have pressed R/S already, press XEQ C ENTER to return to the main menu, and then press 2 R/S to select the delete data option. This will delete the last data pair entered, and return you to data entry mode (the X-register will contain the number of points entered, which will be one less than it was previously, and the Y-register will contain the y value of the point just deleted).

Curve Fitting

If you’re still in data entry mode, press XEQ C ENTER to return to the main menu. Then press 3 R/S to display the curve fitting menu:

The menu choices are:

  1. LINear
  2. LOGarithmic
  3. EXPonential
  4. POWer
  5. Best Fit

Select the type of curve you want by pressing the corresponding number, followed by R/S. If you select best fit (5 R/S), the program will run for a few seconds to find the best fit. If you select a model that is disallowed by your data (for example, a negative y data value rules out the exponential and power curves), the program will display INVALID MODEL. Pressing R/S will take you back to the curve fitting menu for another try.

Next, the curve type you or the program chose will be displayed (one of LIN, LOG, EXP, or POW). Press R/S to continue.

The program will then display the value of m for the chosen curve type. For example, M= -25.94960. Press R/S to continue.

Next the program will display the corresponding b value. For example, B= 84.94137. Once again, press R/S to continue.

Finally the absolute value of correlation coefficient r is displayed. For example, R= 0.99973. Pressing R/S one last time will return you to the main menu.

Pressing R/S without selecting a choice from the curve fitting menu will return you to the main menu.

Predicting x Given y

From the main menu, press 4 R/S to go to x-prediction mode. The program will prompt you with Y?. Enter a y value and press R/S. The corresponding x value will be displayed. For example, X= 23.51674. Press R/S again to be prompted for another y value, or press XEQ C ENTER to return to the main menu.

Predicting y Given x

From the main menu, press 5 R/S to go to y-prediction mode. The program will prompt you with X?. Enter an x value and press R/S. The corresponding y value will be displayed. For example, Y= 4.73007. Press R/S again to to be prompted for another x value, or press XEQ C ENTER to return to the main menu.

Other Statistics

This program uses the HP 35s’ built-in statistics registers (n, Σx, etc.) to accumulate the linear coefficients, the same way the built-in statistics functions do. This means you can do the following at any time while using this program:

  • Perform a linear fit to your data and make predictions using it via the yellow shift L.R menu.
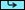
  • Examine the stored linear coefficient sums with the blue shift SUMS menu.
  • Determine the x and y means using the yellow shift x,y menu.
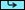
  • Compute the x and y sample and population standard deviation with the blue shift s,σ menu.

Program Listing

Line Instruction Comments
C001♦   LBL C  Display main menu
C002  CLx   
C003  SF 10   
C004  EQN 1+ 2− 3F 4x^ 5y^  Note: x^ and y^ are from the L.R menu
C005  CF 10   
C006  x=0?  Decode menu choice
C007  RTN   
C008  1   
C009  x=y?   
C010  GTO C034  Go to data entry
C011  R↓   
C012  2   
C013  x=y?   
C014  GTO C029  Undo previous entry
C015  R↓   
C016  3   
C017  x=y?   
C018  GTO C101  Go to curve fit menu
C019  R↓   
C020  4   
C021  x=y?   
C022  GTO C200  Go to forecast x
C023  R↓   
C024  5   
C025  x=y?   
C026  GTO C213  Go to forecast y
C027  XEQ C226  Invalid command
C028  GTO C001  Return to main menu
C029♦   RCL Y  Recall previous entry
C030  RCL X   
C031  SF 0  Set removal flag
C032  Σ−   
C033  GTO C048  Go to data add routine
C034♦   n  Get number of data points
C035  x≠0?   
C036  GTO C046  Jump to data entry if not first point
C037  STO P  Clear extended sigma registers
C038  STO Q   
C039  STO S   
C040  STO T   
C041  STO U   
C042  STO V   
C043  STO W   
C044  CF 3  No curve type ruled out yet
C045  CF 4   
C046♦   STOP  Stop for data input, displaying n
C047  Σ+  Add data to built-in sigma registers
C048♦   R↓  Add data to extended sigma registers
C049  STO Y   
C050  x≤0?   
C051  SF 4  Rule out exponential and power
C052  ENTER   
C053  ENTER   
C054  LASTx   
C055  STO X   
C056  x≤0?   
C057  SF 3  Rule out logarithmic and power
C058  x>0?   
C059  LN   
C060  FS? 0   
C061  +/−   
C062  STO+ P  Accumulate ln(x)
C063  LASTx   
C064  R↑   
C065  x>0?   
C066  LN   
C067  FS? 0   
C068  +/−   
C069  STO+ S  Accumulate ln(y)
C070  x2   
C071  FS? 0   
C072  +/−   
C073  STO+ T  Accumulate ln(y)2
C074  R↓   
C075  LASTx   
C076  ×   
C077  STO+ U  Accumulate x ln(y)
C078  R↓   
C079  ENTER   
C080  ENTER   
C081  LASTx   
C082  ×   
C083  FS? 0   
C084  +/−   
C085  STO+ W  Accumulate ln(x) ln(y)
C086  R↓   
C087  x2   
C088  FS? 0   
C089  +/−   
C090  STO+ Q  Accumulate ln(x)2
C091  R↓   
C092  LASTx   
C093  ×   
C094  STO+ V  Accumulate y ln(x)
C095  R↓   
C096  CF 0   
C097  GTO C034  Prepare to fetch next data pair
C098♦   SF 10  Message for ruled out models
C099  EQN INVALID MODEL   
C100  CF 10   
C101♦   CLx  Curve fitting menu
C102  SF 10   
C103  EQN 1L 2G 3E 4P 5B   
C104  CF 10   
C105  x=0?  Decode curve fitting choice
C106  GTO C001  Return to main menu
C107♦   CF 1  Set flags for linear fit
C108  CF 2   
C109  1   
C110  x≠y?   
C111  GTO C116  User didn’t select linear
C112  SF 10   
C113  EQN LIN   
C114  CF 10   
C115  GTO C193  Compute linear coefficients
C116♦   R↓   
C117  2   
C118  x≠y?   
C119  GTO C127  User didn’t select logarithmic
C120  FS? 3  Is logaraithmic fit allowed?
C121  GTO C098  Invalid model
C122  SF 1  Set flags for logarithmic fit
C123  SF 10   
C124  EQN LOG   
C125  CF 10   
C126  GTO C193  Compute logarithmic coefficients
C127♦   R↓   
C128  3   
C129  x≠y?   
C130  GTO C138  User didn’t select exponential
C131  FS? 4  Is exponential fit allowed?
C132  GTO C098  Invalid model
C133  SF 2  Set flags for exponential fit
C134  SF 10   
C135  EQN EXP   
C136  CF 10   
C137  GTO C193  Compute exponential coefficients
C138♦   R↓   
C139  4   
C140  x≠y?   
C141  GTO C152  User didn’t select power
C142  FS? 3  Is power fit allowed?
C143  GTO C098  Invalid model
C144  FS? 4  Is power fit allowed?
C145  GTO C098  Invalid model
C146  SF 1  Set flags for power fit
C147  SF 2   
C148  SF 10   
C149  EQN POW   
C150  CF 10   
C151  GTO C193  Compute power coefficients
C152♦   R↓   
C153  5   
C154  x=y?   
C155  GTO C158  User selected best fit
C156  XEQ C226  Invalid command
C157  GTO C101  Return to curve fitting menu
C158♦   CF 1  Compute correlation for linear
C159  CF 2   
C160  1   
C161  STO M   
C162  XEQ C301   
C163  SF 1  Compute correlation for logarithmic
C164  FS? 3  …but only if logarithmic allowed
C165  GTO C172  Skip power, straight to exponential
C166  XEQ C301   
C167  x<y?  Choose the better of the two
C168  GTO C171   
C169  2   
C170  STO M   
C171♦   x↔y   
C172♦   SF 2  Compute correlation for power
C173  FS? 4  …but only if power allowed
C174  GTO C191  Exponential isn’t allowed either
C175  FS? 3   
C176  GTO C183  Try exponential
C177  XEQ C301   
C178  x<y?  Choose the better of the two
C179  GTO C182   
C180  4   
C181  STO M   
C182♦   x↔y   
C183♦   CF 1  Compute correlation for exponential
C184  FS? 4  …but only if exponential allowed
C185  GTO C191   
C186  XEQ C301   
C187  x<y?  Choose the better of the two
C188  GTO C191   
C189  3   
C190  STO M   
C191♦   RCL M  Set up for best fitting curve
C192  GTO C107   
C193♦   XEQ C285  Compute m (slope)
C194  XEQ C290  Compute b (intercept)
C195  XEQ C301  Compute r (correlation coefficient)
C196  VIEW M  Display m, b, and r
C197  VIEW B   
C198  VIEW R   
C199  GTO C001  Return to main menu
C200♦   INPUT Y  Input y to forecast x
C201  FS? 2   
C202  LN   
C203  RCL B   
C204  FS? 2   
C205  LN   
C206  −   
C207  RCL÷ M   
C208  FS? 1   
C209  ex   
C210  STO X  Store and dispaly result
C211  VIEW X   
C212  GTO C200  Prompt for another y value
C213♦   INPUT X  Input x to forecast y
C214  FS? 1   
C215  LN   
C216  RCL× M   
C217  RCL B   
C218  FS? 2   
C219  LN   
C220  +   
C221  FS? 2   
C222  ex   
C223  STO Y  Store and display result
C224  VIEW Y   
C225  GTO C213  Prompt for another x value
C226♦   SF 10  Error for invalid menu choice
C227  EQN INVALID CMD   
C228  CF 10   
C229  RTN   
C230♦   FS? 1  Recall appropriate Σ x for model
C231  GTO C234   
C232  Σx   
C233  RTN   
C234♦   RCL P  Σ ln(x)
C235  RTN   
C236♦   FS? 1  Recall appropriate Σ x2 for model
C237  GTO C240   
C238  Σx2   
C239  RTN   
C240♦   RCL Q  Σ ln(x)2
C241  RTN   
C242♦   FS? 2  Recall appropriate Σ y for model
C243  GTO C246   
C244  Σy   
C245  RTN   
C246♦   RCL S  Σ ln(y)
C247  RTN   
C248♦   FS? 2  Recall appropriate Σ y2 for model
C249  GTO C252   
C250  Σy2   
C251  RTN   
C252♦   RCL T  Σ ln(y)2
C253  RTN   
C254♦   FS? 1  Recall appropriate Σ xy for model
C255  GTO C262   
C256  FS? 2   
C257  GTO C260   
C258  Σxy   
C259  RTN   
C260♦   RCL U  Σ x ln(y)
C261  RTN   
C262♦   FS? 2   
C263  GTO C266   
C264  RCL V  Σ y ln(x)
C265  RTN   
C266♦   RCL W  Σ ln(x) ln(y)
C267  RTN   
C268♦   XEQ C230  Σ x
C269  XEQ C242  Σ y
C270  ×   
C271  n   
C272  ÷   
C273  +/−   
C274  XEQ C254  Σ xy
C275  +   
C276  RTN  Return Σ xy – Σ x Σ y / n
C277♦   XEQ C230  Σ x
C278  x2   
C279  n   
C280  ÷   
C281  +/−   
C282  XEQ C236  Σ x2
C283  +   
C284  RTN  Return Σ x2 – (Σ x)2 / n
C285♦   XEQ C268  Σ xy – Σ x Σ y / n
C286  XEQ C277  Σ x2 – (Σ x)2 / n
C287  ÷   
C288  STO M   
C289  RTN  Return slope (m)
C290♦   XEQ C230  Σ x
C291  RCL× M   
C292  +/−   
C293  XEQ C242  Σ y
C294  +   
C295  n   
C296  ÷   
C297  FS? 2   
C298  ex   
C299  STO B   
C300  RTN  Return intercept (b)
C301♦   XEQ C268  Σ xy – Σ x Σ y / n
C302  x2   
C303  XEQ C277  Σ x2 – (Σ x)2 / n
C304  ÷   
C305  XEQ C242  Σ y
C306  x2   
C307  n   
C308  ÷   
C309  +/−   
C310  XEQ C248  Σ y2
C311  +   
C312  ÷   
C313  √x   
C314  STO R   
C315  RTN  Return correlation coefficient (r)

Length: 1023, Checksum: EC35

Registers and Flags

Register Use
B Coefficient b (intercept)
M Coefficient m (slope)
P Σ ln(x)
Q Σ ln(x)2
R Correlation coefficient r
S Σ ln(y)
T Σ ln(y)2
U Σ x ln(y)
V Σ y ln(x)
W Σ ln(x) ln(y)
X Last entered or predicted x
Y Last entered or predicted y
Σx Σ x
Σx2 Σ x2
Σy Σ y
Σy2 Σ y2
Σxy Σ xy
n Number of data points
Flag Meaning
0 Set during removal of previous data pair
1 Logarithmic or power model selected
2 Exponential or power model selected
3 Logarithmic and power models disallowed
4 Exponential and power models disallowed
10 Set temporarily to use equations as prompts

Revision History

2007-Oct-17 — Initial release.

2007-Dec-16 — Changed x-prediction and y-prediction routines to prompt for further y or x input respectively instead of returning to the main menu each time. Use XEQ C ENTER to return to the menu. I’ve found this to be more convenient than having to repeatedly select option 4 or 5 from the main menu when making multiple predictions.

Why I Wrote this Program

One of my first programmable calculators was a Texas Instruments SR-52 that I purchased at Eaton’s for $149 back in 1978 or so. At that time, the TI-59 had already been introduced and the store was clearing out the SR-52. This calculator had 224 steps of program memory, 20 registers, and a magnetic card reader. It was only slightly less powerful than the HP-67.

One of the programs in the very comprehensive SR-52 programming manual was a curve fitting program somewhat like the one presented here, except that it only supported linear and exponential curves, and one had to choose the curve type before entering data. What was interesting about this program was that it was presented in great detail, complete with the design processes that went into it. It was the study of TI’s program and the design methods that made me really comfortable with programming their calculator. And of course, the program was useful.

Now, almost 30 years later, an expanded version of this program came to mind as an ideal first project on the HP 35s, especially since my earlier HP calculators (41CX with Advantage Pac, and 42S) had this capability built in. A curve fitting tool such as this one is useful in some of my other work, such as the development of MotoCalc when I’m trying to determine a mathematical model to fit empirical data.

Related Articles

If you've found this article useful, you may also be interested in:

Leave a Comment

22 Comments

  1. Ed Look
    October 18, 2007

    Stefan, thank you! I’ll try to use your HP-35s program to teach myself about how to write a curve fitting program in general, and then I’ll try to write one for myself in FORTRAN.

  2. Paul Becker
    December 15, 2007

    Excellent work. Curve fitting is the one feature I just can’t live without and why I’m always forced to also carry around my bulky 48G. I really like the 48G, but I prefer the 35S’ size and layout. I sure wish HP would bring back the 15C with 35S guts inside. This addition makes my new 35S almost perfect. Thanks again for the effort.

  3. Sam Levy
    January 20, 2008

    I had a concept of using the dual registers to store data in raw form and afterward process for curve fitting. My 35S is in the mail. I too miss the built in Regression program, I solved a nasty problem with it. I gave a kid an $11 Casio that had 6 regression modes in ROM. In addition to the 4 above it added quadratic and inverse.

  4. Mark Lee
    January 23, 2008

    Great idea! One of the features of the HP-41c Advantage Pac that I miss (my 41c is dead).

    However, after inputing and carefully checking the program line-by-line, I’m getting a divide by 0 error message and the checksum does not match your published value. Could there be a typo in the posted program lines?

  5. Stefan Vorkoetter
    January 24, 2008

    Mark, it’s not likely that there’s an error in the listing, because I entered the program from the listing, not the other way around. Unfortunately, the checksum on the HP 35s is rather unreliable; identical programs can yield different checksums on different calculators, so it’s not much help.

    I’d suggest doing a line-by-line comparison (starting with checking that the total number of lines is the same). Where in the program does the division by zero error happen?

  6. Stefan Vorkoetter
    April 05, 2008

    I just rechecked the program against the listing, and the listing is indeed correct. However, the listed checksum was wrong, and I’ve corrected it in the article (it should be EC35).

  7. Miguel De Maria
    April 17, 2008

    Dear Stefan,

    What is x⇔y in line 171? Is it x<>y ?

    Thank you very much!

  8. Stefan Vorkoetter
    April 17, 2008

    It is the "exchange x and y" function. I used the notation x⇔y instead of x<>y because the latter could be confused with x≠y (since <> is used in many programming languages to mean "not equal").

  9. Stefan Vorkoetter
    April 24, 2008

    Miguel, I now see the reason for your confusion. The symbol that I used was a double-ended double-line arrow, but in Internet Explorer, it displays as a square box. I never noticed this because I use Firefox. I have changed it to a double-ended single-line arrow (x↔y), which IE seems to display correctly.

  10. Miguel De maria junior
    May 10, 2008

    Thank you Stefan.

    The program works very well! But in my 35s the CK returns BE21 and I’ve already checked every step twice!

    But no problem.

  11. Razvan Ionescu
    October 18, 2008

    Thank you! Nice program, especially the menus! It works just fine, although the checksum is 6898 on my 35s.

  12. Bill
    March 03, 2009

    I really want to get your program up and running on my 35s. There is one input line I can’t figure out,&#8721;x. I can find &#8721;+ and &#8721;- but not just plain old &#8721;. Any guidance is much appreciated.

  13. Antonio Carlos R. Troyman
    December 31, 2009

    It’s been a log time since the last post you have here, but I have just bought my 35s this month and began exploring it. I already had many calculators since 1973, when I bought my SR-50, an adversary of the HP-35. I saw my engineering mates using many HP calculators but they were too expensives, mainly in Brazil at that time, so I decide to use Texas because they were cheaper. I had an SR-56, a TI-59, then I went to a Sharp PC-1500 (a BASIC pocket computer) that pleased me most, until its display died. Then I decided to buy my first HP, a 49G that was recently launched in 1999. A friend of mine brought it for me from Houston and it was much cheaper than the HP-35 my friends used in the 70’s. I still have it, but it is very hard to program in a serious way (I mean, in SysRPL or in assembler) and very sturdy to carry around. It was then that I saw the advertisements of the HP-35s and I remembered the old HP style, which made me take the decision to have it. At the begining of this month another friend brought me a 35s from Austin and I am very pleased with it (brought me revivals of keystroke programming I missed for some time). Looking for in the internet I found this site of yours and this helped me to discover how easy it is to write programs for it. I wrote curve fitting programs for my PC-1500 which I took from the TI-59 manuals and I used it in many Visual Basic programs I use to code in the University where I work (Federal University fo Rio de Janeiro). After entering your program in my 35s, I also discovered the checksum is different in my machine (I got CK = 2827 and LN = 1024), but the program worked fine, although when I entered other smaller programs from the manual they all matched, maybe beacuse of their short lenghts. Thank you for your pacience in develop this program and making it available for the general public around the world. If you are interested, I am intending to write a program for cubic splines which is very useful as curve fitting also. As soon as I have it done, I will send it to you so you will be free to set it in your site. Best regards, Antonio Carlos

  14. Juha Koskiniemi
    March 21, 2010

    I try to start enter your program, but how to C004 EQN 1+ 2- 3F 4x^ 5y^ is entered? Should it be C004 1+2-3xFx4x^5xy^x so what you actually see in the screen? What is the meaning of L.R menu? And i don’t understand way you take negative root. Should you be in complex mode when negative root is inserted? Cheers.

  15. Stefan Vorkoetter
    March 21, 2010

    Enter it the way it appears in the first screen image in the “Using the Program” section. The L.R. menu is for Linear Regression. The square root key doesn’t work with negative numbers. You have to use the yx key.

  16. Ric Law
    February 04, 2011

    Thank you Stefan for your time and shared knowledge. I just bought this HP35s for my PE exam and never used an HP calculator before. Your are so kind to have posted this curve fitting program, I am amazed that this calculator did not come with it built in considering the cost. HP should give you something for helping their customers out. Seems pretty basic necessity for a “scientific” calculator. Three cheers for you…..I owe you a beer

  17. Mark Brethen
    June 25, 2011

    Wonderful implementation of the Advantage Pac/15c program. Now, I’m used to seeing the straight line fit, for example, as y = a +bx. Is there any reason why I shouldn’t change the labels in the program?

  18. Stefan Vorkoetter
    June 30, 2011

    The output “M=…” is generated automatically by the calculator by the VIEW M instruction. The program uses register M to store the y-intercept value. If you want to change the program to display “A=…”, you’ll have to change all uses of register M to register A. Fortunately, A isn’t being used for anything else by this program, so it’s an easy change to make.

  19. W Jorge
    July 26, 2013

    Thank you for submitting this program for us.

  20. Heath Kocan
    December 04, 2014

    Hello,

    I am fairly new to the 35s and HP’s in general. Your curve fitting tool would help me out with my job a lot. I have one question about the program. Line shows: C034♦ n . Where is the n on the 35s keypad?

    thanks
    HK

  21. Stefan Vorkoetter
    December 05, 2014

    I don’t have the calculator in front of me right not, but I recall that it is on the menu that pops up when you press SUMS.

  22. Vikram Shah
    March 04, 2015

    Hi,

    I just stumbled upon your site looking for more information on HP calculators. What a site you have here!

    I’m interested in watch collecting, slide rules, and of course the HP calcs. Just thought I’d check in – your site is awesome.

    Thanks for sharing your knowledge about this stuff – it’s quality content.
    My favorite has to be this article, and the Aristo Studio Nr. 0970 simulator. I’ve got a 0968.

    –Vikram

Leave a Comment

Want to see your picture next to your comments on this site and others? Visit gravatar.com to register your own globally recognized avatar.

Buy Stefan a coffee! If you've found this article
useful, consider leaving a donation to help support
stefanv.com

Disclaimer: Although every effort has been made to ensure accuracy and reliability, the information on this web page is presented without warranty of any kind, and Stefan Vorkoetter assumes no liability for direct or consequential damages caused by its use. It is up to you, the reader, to determine the suitability of, and assume responsibility for, the use of this information. Links to Amazon.com merchandise are provided in association with Amazon.com. Links to eBay searches are provided in association with the eBay partner network.

Copyright: All materials on this web site, including the text, images, and mark-up, are Copyright © 2024 by Stefan Vorkoetter unless otherwise noted. All rights reserved. Unauthorized duplication prohibited. You may link to this site or pages within it, but you may not link directly to images on this site, and you may not copy any material from this site to another web site or other publication without express written permission. You may make copies for your own personal use.